Треугольники равеы по всем трем признакам.
Объяснение:
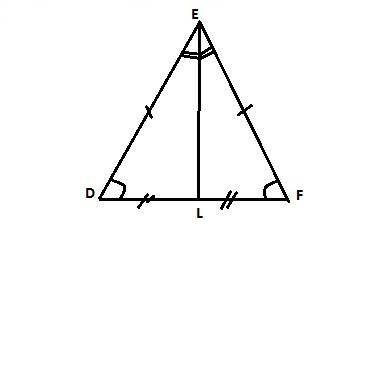
Треугольники DEL и FEL равны по двум сторонам и углу между ними, так как EL - общая сторона, DE=EF (дано), а ∠DEL = ∠FEL (в равнобедренном треугольнике медиана является и биссектрисой. (первый признак)
Или: Треугольники DEL и FEL равны по стороне и двум прилежащим к ней углам, так как DE=EF (дано), ∠EDL = ∠EFL (в равнобедренном треугольнике углы при основании равны), а ∠DEL = ∠FEL (в равнобедренном треугольнике медиана является и биссектрисой. (второй признак).
Или по трем сторонам (третий признак), так как DE=EF (дано), EL - общая, а DL = FL, так как EL - медиана.
Внешний угол треугольника равен сумме двух внутренних, не смежных с ним.
1) Внешний угол треугольника 100°:
∠С + ∠В = 100°
∠C = 100° - ∠B = 100° - 48° = 52°
∠BCA = 52°
2) Внешний угол ∠ABD = ∠С + ∠A = 90° + 46° = 136°
Внешний угол при вершине другого острого угла 136°
3)В равнобедренном треугольнике углы при основании равны.
Внешний угол 140°: ∠A + ∠C = 140°
2∠A = 140° ⇒ ∠A = 140°/2 = 70°
Угол при основании равен 70°
4) Пусть Х = ∠CBK - внешний угол при вершине В,
тогда Х + 64° - внешний угол при вершине А
∠CВA = 180°- Х - смежные углы
∠CAD - по правилу внешнего угла:
∠CAD = ∠C + ∠CBA
X + 64° = 80° + (180° - X)
2X = 196° ⇒ X = 196°/2 = 98°
∠B = ∠CBA = 180°- X = 180° - 98° = 82°
∠B = 82°