Для решения нам нужно найти высоту
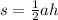
Вот формула площади треугольника. Но так как треугольник прямоугольный, то высота=катет
Здесь используем формулу Пифагора
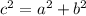
с — гипотенуза, a и b - катеты
Гипотенуза у нас известна, значит используем обратную формулу
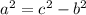
a²=20²-15²=400-225=175
a²=175
Так как в таблице квадратов такого числа нет, значит
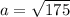
Мы нашли катет, тобишь высоту.
Далее пользуемся формулой площади.
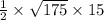
(a — высота, b — основание, по свойствам прямоугольного треугольника)
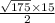
Не думаю, что нужно преобразрвывать, ибо там получится число с большим количеством числел после запятой, если конкретно, то:
99,215674164922147143810590761472265964134
Так что, думаю, лучше оставить формулой (где с дробью)
Можно также ещё преобразовать корень:
(не могу дополнить с формулой, увы, так что "V" = корень, ' — где он заканчивается)
Разбиваем корень на два множителя, один из которых можно будет вычислить.
V175' =V25' × V7`= 5V7'
Пять корней из семи. Значит в том ответе с дробью в числителе можно написать 5V7×15
пусть m – точка пересечения диагоналей ac и bd четырёхугольника abcd. применим неравенство треугольника к треугольникам abc, adc, bad и bcd: ac < ab + bc, ac < da + dc, bd < ab + ad, bd < cb + cd. сложив эти четыре неравенства, получим: 2(ac + bd) < 2(ab + bc + cd + ad).
запишем неравенства треугольника для треугольников amb, bmc, cmd и amd: am + mb > ab, bm + mc > bc, mc + md > cd, ma + md > ad. сложив эти неравенства, получим: 2(ac + bd) > ab + bc + cd + ad.
Дано: A(3;-4), B(1;-1), C(-2;5)
Найти координаты векторов BA и BC
→ →
ВА { 3 -1; -4 +1} или ВА{2; -3}
→ →
BC {-2 -1; 5 +1} или ВС{ -3; 6}