Площадь трапеции равна произведению высоты на полусумму оснований. Если в равнобедренной трапеции диагонали перпендикулярны, то высота равна полусумме оснований. h=(BC+AD):2 ⇒ h(ABCD)=(12+20):2=16 см. S(ABCD)=h•(12+20):2=16•16=256 см².
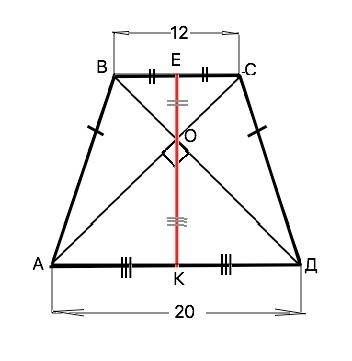
Подробнее: В равнобедренной трапеции диагонали равны. Точкой пересечения они делятся пополам и образуют с основаниями равнобедренные прямоугольные треугольники. Высота каждого из них - медиана и равна половине гипотенузы (соответствующего основания трапеции). ОЕ=ВС/2, ОК=AD/2 Высота трапеции h=ЕК=ЕО+ОК. EK=ВС/2+АD:2, т.е.h= (ВС+AD):2 ⇒S=16•16=256 см²
сторону квадрата можно найти зная его диагональ (сторона равна диагональ /V2) или а-СК/V2 2) диагональ квадрата - бисектриса угла С, а в силу того что треугольник равнобедренный, то и медиана, а то что медиана прямоугольного треугольника проведеная к гипотенузе равна половине гипотенузы - известный факт. Таким образом диагональ квадрата 3D гипотенуза/2 или СК-АВ/2 3) гипотенуза равнобедренного прямоугольного треугольника равна катет*V2 или АВ-АС*V2-BC"V2 Вычисляем: 3 АВ-12 V2 (см) 3+2 > СК-12 /2/2-6V2(см) 3+2+1> а-(6 w2)/(V2)-6 (см)
Без того знака не знаю