21) Один из углов прямоугольного треугольника равен 60, а сумма
гипотенузы и меньшего из катетов равна 26,4 см. Найти гипотенузу
треугольника.
22) Разность двух односторонних углов при пересечении двух
параллельных прямых секущей равна 50 градусам. Найти эти углы.
23) Найдите неразвернутые углы, образованные при пересечении двух
прямых, если сумма двух из них равна 126°.
24) Основание равнобедренного треугольника равно 8см. Медиана,
проведенная к боковой стороне, разбивает треугольник на два
треугольника так, что периметр одного треугольника на 2см больше
периметра другого. Найти боковую сторону данного треугольника.
25) В прямоугольном треугольнике ABC с прямым углом С внешний угол
при вершине А равен 120, AC+AB=18см. Найти AC и AB.
26) Найдите все углы, образованные при пересечении двух
параллельных прямых а и в секущей C , если один из углов на
70° больше другого.
∠ 1 = ?°, на 55° больше, чем ∠ 2.
∠ 2 = ?°
Оба угла являются смежными.
Решение:Пусть x° равен смежный ∠ 2, тогда ∠ 1 равен (55+x)˚. Зная, что свойство смежных углов всегда содержит сумму 180°, составим уравнение с переменными и решим задачу алгебраическим
Составление математической модели:
Работа с математической моделью:
Поскольку уравнение имеет переменные, раскроем скобки и найдём значение переменных:
Теперь, зная что число с переменной и число без переменной в данном случае вычислить невозможно, перенесем число без переменной в правую часть уравнения (число становится отрицательным):
Затем вычислим полученный пример, находящийся в правой части уравнения:
Чтобы найти неизвестный множитель, необходимо произведение разделить на известный множитель:
ответ математической модели:
Исходя из значения данного примера, получим корень уравнения:
Теперь остаётся только узнать величину ∠ 1:
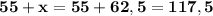 ˚ - ∠ 1.
˚ - ∠ 1.
Проверка: 117,5° + 62,5° = 180° - задача решена верно.ответ: ∠ 1 = 117,5°; ∠ 2 = 62,5°.