1.Отрезки АЕ и ДС пересекаются в точке О, являющейся серединой каждого из них. Доказать, что треугольник АОС равен треугольнику ЕОД.
2.В равнобедренном треугольнике АВС с основанием АС угол В равен 42 градуса. Найти два других угла треугольника АВС.
3.Точки В и Д лежат в разных полуплоскостях относительно прямой АС. Треугольники АВД и АДС равносторонние. Доказать, что АВ параллельна СД УМОЛЯЮ ГОДОВАЯ КР
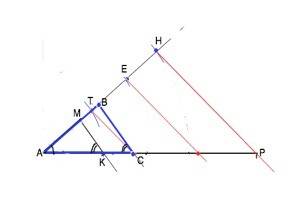
На произвольной прямой откладываем длину АВ заданной стороны.
От т.А как от вершины откладываем с циркуля и линейки данный угол. (Как это делается - есть во многих источниках стандартный).
Т.к. центр вписанной в угол окружности лежит на его биссектрисе, проведем ее ( тоже стандартный деления угла на два равных).
В произвольной точке М на АВ возведем перпендикуляр, на нем отложим длину MP = r радиуса вписанной окружности.
Из т.Р проведем прямую параллельно МА до пересечения с биссектрисой в т.О.
Точка О - центр вписанной окружности, её радиус будет равен заданному и перпендикулярен АВ.
Соединим т.В с т.О.
На ОВ как на диаметре построим окружность радиусом ВО:2. ( как делить отрезок пополам мы помним).
Точки пересечения этой окружности с данной - точки касания касательных. Та, что вне угла, нас не интересует.
Соединим В и найденную точку касания и продолжим ее до пересечения со второй стороной угла. в т.С.
Треугольник построен.