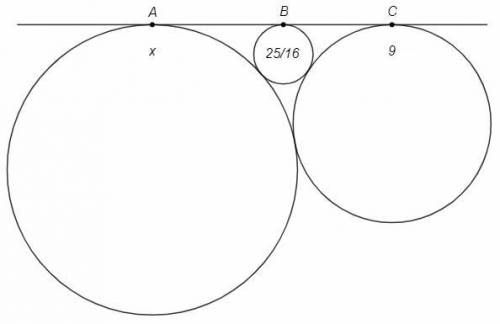
Две окружности касаются внешним образом и имеют общую внешнюю касательную. Найдем расстояние между точками касания на прямой.
Отрезки касательных из одной точки равны (синие отрезки). Центры окружностей лежат на биссектрисах углов, образованных касательными. Угол между биссектрисами смежных углов - прямой. Точка касания окружностей лежит на линии центров. Радиусы, проведенные в точку касания, перпендикулярны касательной. Таким образом синий отрезок является высотой из прямого угла и равен среднему пропорциональному проекций катетов, √(R1*R2).
Расстояние между точками касания на прямой равно 2√(R1*R2).
В задаче три пары аналогичных окружностей.
AB+BC=AC => 2√(x*25/16) +2√(9*25/16) =2√(9x) <=> 7√x =15 <=> x=225/49

Трапеция АВСД, ВС=16, АД=30, точка О ниже АД, соединяем вершины трапеции с центром О, ОА=ОВ=ОС=ОД=17, в треугольнике ВСО проводим высоту ОК , треугольник ВСО равнобедренный, ОВ=ОС=17, ОК - медиана, биссектриса, высота. ВК=СК = 16/2=8
треугольник ОВК прямоугольный, ОК=корень(Ов в квадрате - ВК в квадрате) =
=корень =(289-64)=15
Треугольник ОАД равнобедренный , точка Н - пересечение ОК с АД, высота ОД=медиане биссектрисе, АН=ДН=30/2=15
треугольник ОАН прямоугольный, ОН= корень (АО в квадрате - АН в квадрате)=
=корень(289-225) = 8
КН - высота трапеции = ОК-ОН=15-8=7
Решение на фото......