70
Объяснение:
скорее всего ты ошибся(-лась) и там четырех угольник АВОС.
И так, сначала чертим окружность с центром в точке О. проводим к нет две касательные из точки А (т.к. касательные выходят из одной точки). проводим два радиуса ОВ и ОС, и биссектрису угла О (скажем так, в условии про биссектрису не пишем) ОА. Получим четырехугольник АОВС. так как прямая ОА делит его на два равных треугольника, нам нужно найти одну сторону (либо СА, либо ВА). я искала через треугольник АОВ. нам известен катет и гепотенуза, второй катет ищем через теорему Пифагора ( квадрат гипотенузы равен сумме квадратов катетов). в нашем случае: чтобы найти неизвестный катет нужно от квадрата гнпотенузы отнять квадрат известного катета. далее находим периметр. периметр это сумма длин сторон. значит нам нужно сложить ОС, ОВ, ВА и АС. после сложения получаем 70.
P.S: если здесь я объяснила не понятно, то я прикрепила фото с решением (сорри за почерк)
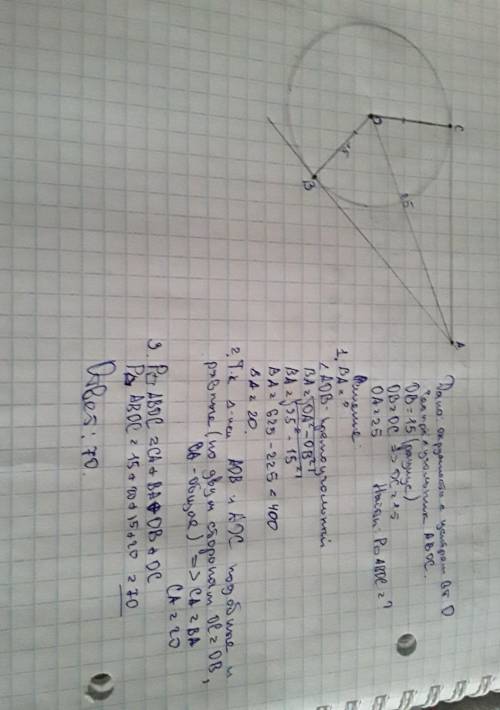
Объяснение:
1. Це клясичний трикутник Піфагора.
Прямий кут між катетами 3 та 4, тобто площа рахується як площа будь-якого прямокутного трикутника: 0.5*3*4=6
2. АВС - також трикутник Піфагора з кутами А=60, B=30, C=90 катетом 3 гіпотенузою 5, а отже іншим катетом 4. Отже площа АВС, рахується як в попередньому завдан і дорівнює 6
3. Уявімо ромб як 2 рівних і тимчасово рівнобедрених трикутника зі стороною a, та із звгальною підставою b, яка є діагоналлю рмба. Площа такого трикутника рахується за формулую:
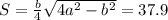
Оскільки трикутників 2 - то S ромба = 37.9*2=75.8
Решим по формуле Герона, хотя зачем, если векторное произведение проще взять.
Итак, жирным обозначены ВЕКТОРА.
MN = (6; 8; 0) a = IMNI = 10;
MT = (6; 0; 2) b = IMTI = 2*√10 (уже весело)
TN = (0; -8; 2) c = ITNI = 2*√17 (еще веселее, может, зря я в это ввязался?)
(Хотя есть же Excel, который мигом сообщил мне ответ S^2 = 676; S = 26;
да и половина векторного произведения MNXMT/2 = (8; - 9; - 24) имеет модуль 26 :)) ну раз так, главное - не спутать корни :)))
Итак, полупериметр
p = 5 + √10 + √17;
p - a = - 5 + √10 + √17;
p - b = 5 - √10 + √17;
p - c = 5 + √10 - √17;
Перемножаем, получим S^2.. в таком порядке p(p-c)(p-b)(p-a);
(5 + √10 + √17)*(5 + √10 - √17)*(5 - √10 + √17)*(√17 - 5 + √10) =
((5 + √10)^2 - 17)*(17 - (5 - √10)^2) =
= 17*(5 + √10)^2 - 17^2 - (5 + √10)^2*(5 - √10)^2 + 17*(5 - √10)^2 =
= 17*(25 + 10)*2 - 17^2 - 15^2 = 676;
ур.
S = √676 = 26