Решим данную задачу обобщённым Начнём с теории:
Если в трапецию вписана окружность, то сумма его оснований равна сумме боковых сторон, BC + AD = AB + CDЕсли около трапеции описана окружность, то сумма его противолежащих углов равна 180°. Это означает, что данная трапеция является равнобокой, AB = CDВ равнобокой трапеции её высота равна диаметру вписанной окружности, BH = d = 2rПо свойству равнобокой трапеции высота, опущенная на бо'льшее основание, делит её на два отрезка, бо'льший из которых равен полусумме оснований, а ме'ньший - полуразности основанийПусть BC = a, AD = b, BH = 2r, тогда HD = (b + a)/2, AH = (b - a)/2
AB + CD = BC + AD = a + b ⇒ AB = CD = (b + a)/2
В ΔABH применим теорему Пифагора: BH² + AH² = AB²
(2r)² + ( (b - a)/2 )² = ( (b + a)/2 )²
Умножаем обе части на 4 и раскрываем скобки:
16r² + b² - 2ab + a² = b² + 2ab + a²
16r² = 4ab ⇒ r² = ab/4 ⇒ r = √(ab)/2 ⇒ BH = d = √ab
В ΔBHD: BD² = BH² + HD² = (2r)² + ( (b + a)/2 )²
4BD² = 16r² + b² + 2ab + a² = b² + 6ab + a²
BD = √(b² + 6ab + a²)/2
В ΔABH: sin∠A = BH/AB = 2r/(b + a)/2 = 4r/(b + a) = 2√(ab)/(b + a)
По теореме синусов в ΔABD: R = BD/(2•sin∠A)
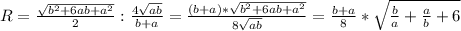
Обобщённая формула для нахождения радиуса описанной около трапеции окружности через известные основания, а и b
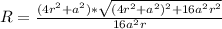
Обобщённая формула для нахождения радиуса описанной окружности через известный радиус вписанной окружности и основание
Подставляем в формулу a = 1 , r = 1,5 и находим искомый радиус:
4r² = (2r)² = 3² = 9 , a² = 1² = 1
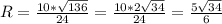
Несложно найти все стороны данной трапеции: BC = 1 , AD = 9 , AB = CD = 5
Также можно заметить, в ΔABH: cos∠A = AH/AB
cos∠A = (b-a)/2 / (b+a)/2 = (b - a)/(b + a)
∠A = ∠D = arccos( (b - a)/(b + a) )
ответ: 5√(34)/6
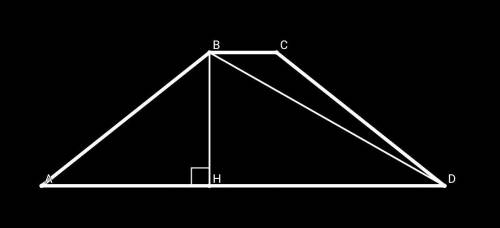
1.в трапецию можно вписать окружность тогда, когда сумма оснований равна сумме боковых сторон.
Следовательно, можно найти вторую боковую сторону:
6+27=13+х
33=13+х
х=33-13
х=20
20 см - вторая боковая сторона
2. Радиус вписанной окружности в трапецию равен половине высоты трапеции.
Высота трапеции неизвестна. Её можно узнать, найдя площадь трапеции.
Формула площади трапеции по четырем сторонам :
подставляем все значения в эту формулу, учитывая, что а=6, б=27см, с=13 см, д=20 см, и находим площадь, которая равна 198 см2.
3. Ну а теперь можно приступить к нахождению высоты, зная площадь и основания.
У нахождения площади также существует формула: (а+б)/2*высоту
Подставляем все известные значения.
(6+27)/2*высоту=198
33/2*высоту=198
высота=198*2/33
Высота равна 12 см.
4. Радиус круга: 12/2 = 6 см.
О т в е т: 6 см