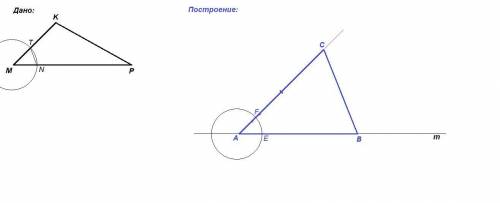
1. На прямой m отложим отрезок АВ = МР.
2. Построим ∠А = ∠М. Для этого:
построим окружность произвольного радиуса с центром в точке М; точки пересечения этой окружности со сторонами угла М обозначим N и Т;
построим окружность с тем же радиусом с центром в точке А; Е - точка пересечения этой окружности с отрезком АВ;проведем дугу с центром в точке Е и радиусом, равным NT; F - точка пересечения дуги с окружностью;проведем луч AF.3. На луче AF дважды последовательно отложим отрезок, равный МК, получим точку С.
4. Соединим точки В и С.
ΔАВС - искомый.
Задача может не иметь решения, если в данном треугольнике сторона МК большая и не выполняется неравенство:
2MK < MP + KP.
294
Объяснение:
косинус угла равен отношению прилежащего катета к гипотенузе,
если х это гипотенуза, то прилежащий катет к углу А равен 0,8х
тогда (0,8х)²+441=х²
0,36х²=441
х²=1225
х=35
значит второй катет равен 0,8*35=28
площадь тр-ка равна 1/2*28*21=294