1. Периметр соевого сечения конуса равен 360 ед.
2. Объем конуса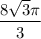 
ед.³
Объяснение:
Требуется найти:
1. Периметр соевого сечения конуса.
2. Объем конуса.
498.
Дано: Конус.
АК = 100; sin∠АКО = 0,6.
Найти: Р (КАМ)
1. Рассмотрим ΔКАО - прямоугольный.
Синус угла - отношение противолежащего катета к гипотенузе.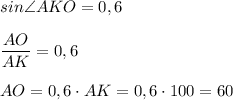
По теореме Пифагора:
КО² = АК² - АО²
КО² = 10000 - 3600 = 6400
КО = 80
⇒ КМ = 80 · 2 = 160
Р (КАМ) = АК + АМ + КМ = 100 + 100 + 160 = 360 (ед.)
504.
Дано: Конус;
r = СО = 2; ∠ВСО = 60°;
Найти: V конуса.
Объем конуса найдем по формуле:
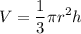, где r - радиус основания, h - высота конуса.
1. Рассмотрим ΔСВО - прямоугольный.
Тангенс угла - отношение противолежащего катета к прилежащему.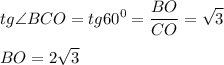
2. Найдем объем:
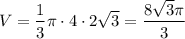(ед.³)
60 градусов = (1х+3х)/2
где 1 и 3 - заданные условием задачи части; х - градусная мера 1 части.
Отсюда
х= 60*2/4 = 30 градусов - это градусная мера меньшей дуги АС
30 градусов *3 = 90 градусов - это градусная мера большей дуги ДВ
Проверяем правильность решения:
На дугу в 30 градусов опирается вписанный угол В, который равен = 1/2 дуги АС равной 30 => угол В = 15
На дугу в 90 градусов опирается угол В = 1/2 дуги ДВ равную 90 =>
угол Д = 45
Следовательно сумма углов треугольника АОВ = 45+15+120 =180, где О центр пересечения хорд
Задача решена
ответ: градусная мера дуг, заключенных между сторонами угла 60 градусов равна 30 и 90 градусам.