(см. объяснение)
Объяснение:
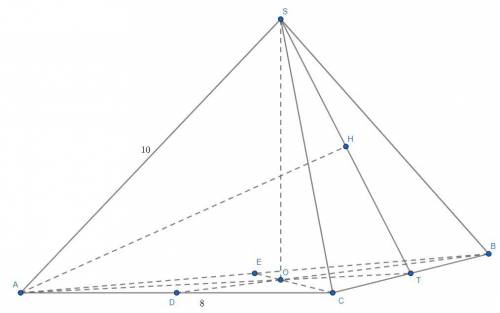
Рассмотрим плоскость (AST). Заметим, что BC⊥(AST), так как BC⊥SO и BC⊥AT и SO∩AT=O. Тогда BC перпендикулярна любой прямой, лежащей в этой плоскости. Опустим теперь перпендикуляр AH из точки A на ST в плоскости (AST). Получим, что AH⊥ST и AH⊥BC и ST∩BC=T. Тогда AH⊥(BSC), т.е. является искомым расстоянием. Найдем теперь AH. Приравняв площади треугольника, получим, что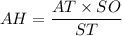 
. Понятно, что AT ищем по теореме Пифагора для треугольника ATC: AT²=AC²-TC², => AT=4√3. ST ищем по той же теореме Пифагора, но для треугольника STC: ST²=SC²-TC² => ST=2√21. Перед тем, как искать SO, вспомним, что медианы точкой пересечения делятся 2:1, считая от вершины. Тогда OT=4/√3 => SO=2√177/3 (опять-таки по теореме Пифагора для треугольника OST). Значит 
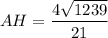. Приведем теперь ответ к требуемому виду: 
.
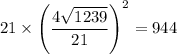Задание выполнено!
Пусть дано ΔАВС i ΔА 1 В 1 С 1 причем АС = А 1 С 1 , ВМ i B 1 M 1 - медианы, ВМ = B 1 M 1 , ∟BMC = ∟B 1 M 1 C 1 .
Докажем, что ΔАВС = Δ А 1 В 1 С 1 .
Рассмотрим ΔВМС i ΔB 1 M 1 C 1 .
1) ВМ = B 1 M 1 (по условию)
2) ∟BMC = ∟В 1 М 1 С 1 (по условию)
3) МС = М 1 С 1 (половины равных стopiн AC i A 1 С 1 ).
Итак, ΔВМС = ΔВ1М1С1 за I признаку.
Рассмотрим ΔАВС i Δ А 1 В 1 С 1 .
1) AC = А 1 С 1 (по условию)
2) ∟C = ∟C 1 (т. К. ΔВМС = Δ B 1 M 1 C 1 )
3) ВС = В 1 С 1 (т. К. ΔВМС = Δ B 1 M 1 C 1 ).
Итак, ΔАВС = ΔА 1 В 1 С 1 , за I признаку.