уол ВАС= СAD=30( нактрест., ВС||AD, ас секущая) если вокруг трапеции можно описать окружность, то трапеция равно бедренная. Угол D=ВАС+СAD, ВАС=СAD=30-ас бисектрисса, угол D=30+30=60,
S=4r^2/sinD
S=256*2/ корнь из 3,
S=512/корнь из 3
Найдем второй отрезок гипотенузы для каждого случая.
Высота прямоугольного треугольника, проведенная из вершины прямого угла, есть среднее пропорциональное для отрезков, на которые делится гипотенуза этой высотой.⇒
a)
СD²=АD•ВD
16=4•BD
BD=16:4=4⇒
Высота СD - медиана и биссектриса ∆ АВС и делит его на два равнобедренных прямоугольных треугольника.
Острые углы такого треугольника равны 45°
б)
СD²=АD•ВD
16=4√3•BD⇒
BD=16:4√3=4/√3
Из ∆ САD:
tg∠САD=CD:AD=4:4√3=1/√3- это тангенс 30°
Из ∆ CВD:
tg∠СBD=BD:CD=(4/√3):4=√3 - это тангенс 60°
Острые углы этого треугольника 30° и 60°
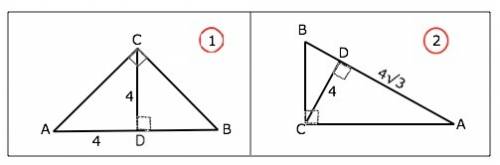
Найдем второй отрезок гипотенузы для каждого случая.
Высота прямоугольного треугольника, проведенная из вершины прямого угла, есть среднее пропорциональное для отрезков, на которые делится гипотенуза этой высотой.⇒
a)
СD²=АD•ВD
16=4•BD
BD=16:4=4⇒
Высота СD - медиана и биссектриса ∆ АВС и делит его на два равнобедренных прямоугольных треугольника.
Острые углы такого треугольника равны 45°
б)
СD²=АD•ВD
16=4√3•BD⇒
BD=16:4√3=4/√3
Из ∆ САD:
tg∠САD=CD:AD=4:4√3=1/√3- это тангенс 30°
Из ∆ CВD:
tg∠СBD=BD:CD=(4/√3):4=√3 - это тангенс 60°
Острые углы этого треугольника 30° и 60°

Раз можно описать окружность, значит трапеция равнобедренная.
Далее, угол АСВ = угол САD = угол САВ = 30 градусов. Поэтому угол при основании 60, а АС перпендикулярно CD. Поэтому АD - диаметр окружности, а CD = радиусу, ВС = АС/2. Это проще всего "увидеть", если продлить АВ и CD до пересечения, пусть это точка К. Тогда СD = DK/2 (С - основание высоты ADK), и ВС - средняя линяя в ADK.
Можно сразу сказать, что площадь трапеции равна 3/4 от площади равностороннего треугольника (ADK) со стороной, равной диаметру 16.
S = (3/4)*(1/2)*16^2*(корень(3)/2) = 48*корень(3)
Девушке из предыдущего решения :))) - S = (1/2)*a*b*sin(C) - это формула площади (С - угол между а и b)...
которая, кстати, получается потому, что Hb (высота к b) = a*sin(C)