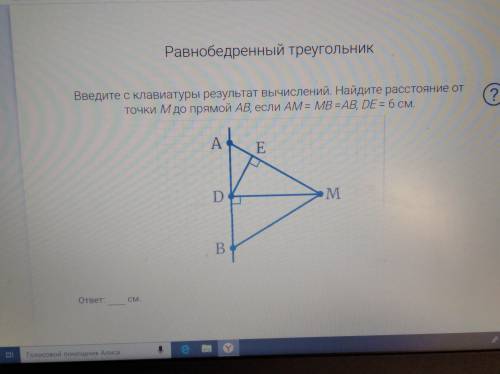
Дано:
треугольник АМВ.
АМ = АВ = МВ.
DE = 6 см
Найти:
S от М до АВ
Так как МВ = АМ = АВ => треугольник АМВ - равносторонний.
А так как треугольник АМВ - равносторонний => этот треугольник ещё и равнобедренный.
Сумма углов треугольника равна 180°
∠А = ∠М = ∠В = 180°/3 = 60° (треугольник АМВ - равносторонний)
Так как треугольник АМВ - равнобедренный => MD - высота, медиана, биссектриса
=> ∠AMD = ∠BMD = 60˚/2 = 30˚
Если угол прямоугольного треугольника равен 30°, то напротив лежащий катет равен половине гипотенузы.
=> MD = 2DE
MD = 6 * 2 = 12 см
(MD - и есть расстояние от М до АВ)
ответ: 12 см.
Дано:
АВС - треугольник
АМ = СМ
уг. АВС = 60°
уг. ВМА = 90°
Найти
уг. МВС - ?
уг. ВСА - ?
Решение
угол ВМА = 90° => уг. ВМС = 90°
т.е. ВМ | АС, а значит,
ВМ - высота, проведенная из вершины В на АС.
Также АМ = МС, а значит
ВМ - медиана, проведенная из вершины В на АС.
Если медиана треугольника является его высотой, то этот треугольник - равнобедренный.
ВМ - высота и медиана ∆АВС, =>
=> ∆АВС - равнобедренный, основание АС =>
=> ВМ - также является биссектрисой ∆АВС, т.е.
уг. АВМ = уг. СВМ
Так, как ∆АВС - равнобедренный, с основанием АС, то углы при основании - равны друг другу
уг. ВАС = уг. АСВ
и равны
угол ВАС = угол ВСА = 1/2 • (180 - угол АВС)
угол ВАС = угол ВСА = 1/2 • (180 - 60) = 60°
а значит ∆АВС - равносторонний.
угол MBC = 30°
угол ВCA = 60°
Відповідь:
При параллельному перенесенні точку (-1, -1) буде перенесено у точку (0, -3).
Пояснення:
При параллельному перенесенні точки (3, 5) вона переноситься у точку (4, 3).
При цьму координата х збільшується на одиницю, а координата у зменьшується на дві одиниці.
4 - 3 = 1 - зміна координати х.
3 - 5 = -2 - зміна координати у.
Такі ж самі зміни при параллельному перенесенні відбудуться і з точкою (-1, -1).
-1 + 1 = 0 - координата х після перенесення.
-1 + (-2) = -3 - координата у після перенесення.
При параллельному перенесенні точку (-1, -1) буде перенесено у точку (0, -3).
ответ: 12 см
Объяснение:
3)Т.к. треугольник АВМ равносторонний, то все углы = 60 градусов, МD - биссектриса и высота => угол ЕМD = 60:2 = 30 градусов.
В прямоугольном треугольнике DEM катет DE = половине гипотенузы DM => DM = 6*2=12 см
ответ: 12 см