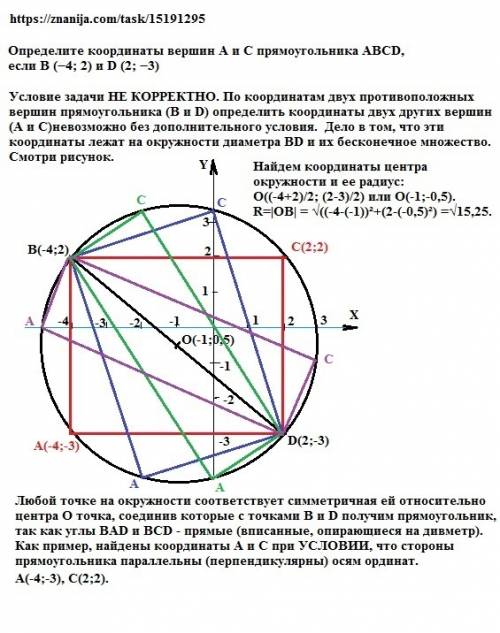
Условие задачи НЕ КОРРЕКТНО. По координатам двух противоположных вершин прямоугольника (B и D) определить координаты двух других вершин (А и С) невозможно без дополнительного условия. Дело в том, что вершины прямоугольника лежат на окружности диаметра BD и их бесконечное множество.
Смотри рисунок.
Любой точке на окружности соответствует симметричная ей относительно центра О точка, соединив которые с точками В и D получим прямоугольник, так как углы ВАD и ВСD - прямые (вписанные, опирающиеся на дивметр).
Найдем координаты центра окружности, описанной около данного прямоугольника и ее радиус:
О((-4+2)/2; (2-3)/2) или О(-1;-0,5).
R=|ОВ| = √((-4-(-1))²+(2-(-0,5)²) =√15,25. Тогда уравнение окружности (x+1)² + (y+0,5)² =15,25.
ЛЮБАЯ точка на этой окружности - вершина А, симметричная ей относительно центра О точка - вершина С.
Найдем координаты вершин А и С ПРИ УСЛОВИИ, что стороны прямоугольника параллельны осям ординат.
В уравнение окружности подставим координату Х=-4 и найдем для нее соответствующую координату Y: (-3)² + (y+0,5)² =15,25. => Y² + Y -6 = 0. => Y1=3, Y2=-2. Точно так же для точек с координатой Х=2. Y1=2 и Y2=-3. Тогда имеем: А(-4;-3) и С(2;2).
А₁А₂ = 2 см
Объяснение:
Если две параллельные плоскости пересечены третьей, то линии пересечения параллельны.
Пересекающиеся прямые А₁В₁ и А₂В₂ задают плоскость, которая пересекает плоскости α и β по прямым А₁А₂ и В₁В₂, значит
А₁А₂ ║ В₁В₂.
Тогда ∠МВ₁В₂ = ∠МА₁А₂ как накрест лежащие при пересечении параллельных прямых А₁А₂ и В₁В₂ секущей А₁В₁,
∠В₁МВ₂ = ∠А₁МА₂ как вертикальные, значит
ΔВ₁МВ₂ подобен ΔА₁МА₂ по двум углам.
МВ₂ = А₂В₂ - МА₂ = 10 - 4 = 6 см
Пусть А₁А₂ = х, тогда В₁В₂ = х + 1,
6x = 4(x + 1)
6x = 4x + 4
2x = 4
x = 2
А₁А₂ = 2 см