7. BM = (1/4)·(a+c) - b.
8. D = √13 ед.
Объяснение:
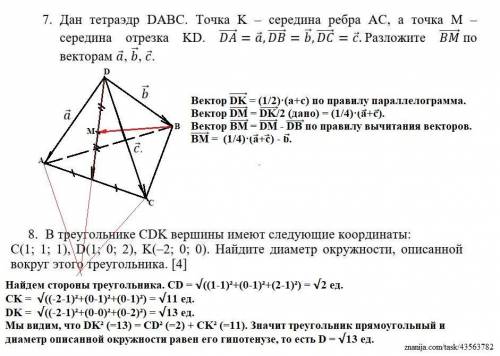
7. Вектор DK = (1/2)·(a+c) по правилу параллелограмма (АК=КС).
Вектор DM = DK/2 (дано) = (1/4)·(a+c).
Вектор ВМ = DM - DB по правилу вычитания векторов.
BM = (1/4)·(a+c) - b.
8. Найдем стороны треугольника. CD = √((1-1)²+(0-1)²+(2-1)²) = √2 ед.
CK = √((-2-1)²+(0-1)²+(0-1)²) = √11 ед.
DK = √((-2-1)²+(0-0)²+(0-2)²) = √13 ед.
Мы видим, что DK² (=13) = CD² (=2) + CK² (=11). Значит треугольник прямоугольный и диаметр описанной окружности равен его гипотенузе, то есть D = √13 ед.
Объяснение:
1) неверно, поскольку у остроугольного треугольника все 3 угла острые
2) Да, существует, поскольку сумма углов треугольника составляет 180°. 170+9+1=180°
3) Не может, потому что в прямоугольном треугольнике 2 катета и одна гипотенуза
4) Нет не может, потому что в этом случае два угла должны быть равны при основании и тогда их сумма составит 90+90=180°, без учёта третьего угла, а сумма всех 3-х углов треугольника составляет 180°, в нашем случае сумма углов получится более 180°
5) Да, если внутренний угол треугольника 30°, тогда внешний угол составит 180–30=150°
6) Нет, поскольку если внешний угол равен 50°, тогда внутренний угол будет равен 180–50=130°. В прямоугольном треугольнике не может быть тупого угла, потому что один угол прямой=90°, а 2 других - острые - менее 90°
7) Нет, не может быть угол 100° в прямоугольном треугольнике, потому что один угол 90°, а остальные острые - меньше 90°
8) Нет, не существует поскольку сумма острых углов прямоугольного треугольника равна 90°, не более.
Объяснение: ЗАДАНИЕ 2
Обозначим вершины треугольника А В С а Высоту ВН. ВН делит ∆АВС на 2 прямоугольных треугольника АВН и СВН, в которых АН, СН и общая высота ВН - катеты, а АВ и ВС - гипотенуза. Пусть АВ=х, тогда ВС=х+3. Так как ВН -общая, то в она будет одной величины для двух треугольников. Составим уравнение используя теорему Пифагора:
АВ²-АН²=ВС²-СН²
х²-5²=(х+3)²-10²
х²+25=х²+6х+9-100 переносим х в левую сторону уравнения, а цифры в правую с противоположными знаками:
х²-х²-6х= -25+9-100
-6х= -66
х= –66/–6
х=11
Итак: АВ=11см, тогда ВС=11+3=14см
АС=5+10=15см
Теперь найдём периметр треугольника зная его стороны:
Р=11+14+15=40см
ответ: б) Р=40см
ЗАДАНИЕ 3
Обозначим вершины ромба А В С Д а точку пересечения диагоналей О. Диагонали ромба пересекаясь делятся на равные отрезки и делят углы пополам. Также они делят ромб на 4 одинаковых прямоугольных треугольника. Поэтому
угол АВО=углу СВО=30°; АО=СО;
ВО=ДО . По условиям ВД=4√3, тогда
ВО=ДО=4√3÷2=2√3см. Рассмотрим ∆АВО. В нём АВ- гипотенуза, а АО и ВО- катеты, угол АВО=30°, катет ВО=2√3см. Пусть АО=х. Катет лежащий напротив угла 30° равен половине гипотенузы, поэтому гипотенуза АВ будет в 2 раза больше катета АО, и будет 2х. Составим уравнение используя теорему Пифагора: АВ²-АО²=ВО²
(2х)²-х²=(2√3)²
4х²-х²=4×3
3х²=12
х²=12÷3
х²=4
х=√4
х=2
Итак: АО=2см, тогда АВ=2×2=4см.
Нам известна сторона ромба, теперь найдём его периметр:
Р=4×4=16см
ответ: а) 16см
ЗАДАНИЕ 4
Обозначим вершины треугольника А В С а биссектрисы других углов СК и АС а точку их пересечения О. Пусть угол С=20°, тогда сумма углов А и С=180-20=160°. Рассмотрим полученный ∆ АОС. Мы нашли сумму углов А и С, и так как их делят биссектрисы пополам, запишем их так: (А+С)/2.
Угол АОС=180-160/2=180-80=100°. Найден тупой угол между биссектриса и, теперь найдём острые углы между ними АОК и СОМ, знаю что сумма углов образуемых при пересечении составляет 360°:
Угол АОК=углу СОМ=(360-2×100)/2=
=(360-200)/2=160/2=80°
ОТВЕТ: в) острый угол между биссектрисами=80°
ЗАДАНИЕ 5
Чтобы найти угол А, воспользуемся теоремой косинусов:
cosA=(a²-b²-c²)/-2ab=(7²-8²-5²)/(-2×8×5)=
=(49-64-25)/-80= -40/-80=1/2
cos1/2=60°
ответ: г) угол А=60°