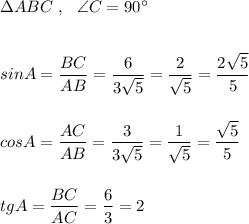
відомо що гіпотенуза АВ=3√5, катет АС=3 в даному випадку цей катет прилеглий до кута α та катет ВС=6 в даному випадку протилежний куту α. потрібно знайти sinα, cosα та tgα.
за означенням відношення прилеглого катета до гіпотенузи дорівнює косинусу даного кута, в нашому випадку cosα = 3/3√5 = 1/√5. Відношення протилежного катета до гіпотенузи дорівнює синусу sinα = 6/3√5 = 2/√5 та тангенс це відношення протилежного катета до прилеглого tgα = 6/3 = 2
Обозначим прямоугольник ABCD и точку пересечения диагоналей O как
B C
E O
A D
Треугольник AOB равнобедренный, поэтому высота OE является и медианой. Тогда, так как AB=14, AE=7. По теореме Пифагора из прямоугольного треугольника AEO находим AO^2=EO^2+AE^2=49+36=85. AO=sqrt(85). Тогда AC=2sqrt(85) и AC^2=4*85=340. Из прямоугольного треугольника ABC по теореме Пифагора BC^2=AC^2-AB^2=340-196=144. Значит BC=12. Тогда площадь прямоугольника равна AB*BC=14*12=168.
ответ:168.
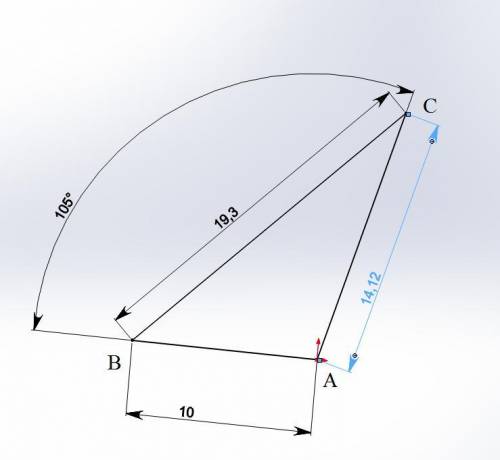
а) ∠С=30°; а=19,3 см; в=14,1 см
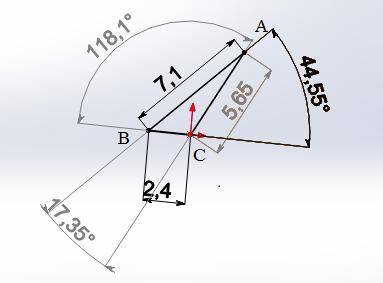
б) в=5,65 см; ∠А=17,35°; ∠С=118,1°
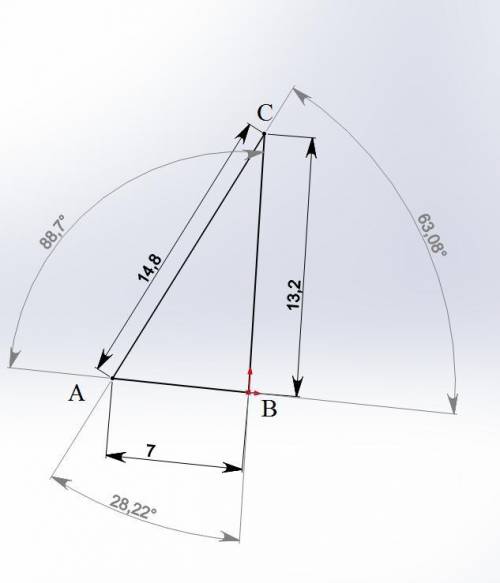
с) ∠А=63,08°; ∠В=88,7°; ∠С=28,22°
Объяснение:
а) ∠А=105°; ∠В=45°; с=10 см
∠С, а, в ?
∠С=180°-105°-45°=30°
а/sin∠А=с/sin∠С=10/sin30°=20
а=20*sin∠А=20*sin105°=19,3 см
в=20*sin∠В=20*sin45°=14,1 см
б) с=7,1 см ; а=2,4 см ; ∠В=44°33'
в, ∠А, ∠С ?
в²= а²+с²-2а*с*cos∠В=2,4²+7,1²-2*2,4*7,1*cos44°33'=31,9
в=5,65 см
sin∠А=sin∠В/в*а=sin44°33'/5,65*2,4=0,3
∠А=17,35°
sin∠С=sin∠В/в*с=sin44°33'/5,65*7,1=0,88
∠С=118,1°
с) а=13,2 см ; в=14,8 см; с=7см
а²=в²+с²-2*в*с*cos∠А
13,2²=14,8²+7²-2*14,8*7*cos∠А
cos∠А=93,8/207,2=0,45;
∠А=63,08°;
sin∠В=sin∠А/а*в=sin63,08°/13,2*14,8=0,9997
∠В=88,7°
sin∠С=sin∠А/а*с=sin63,08°/13,2*7=0,7=0,47
∠С=28,22°