a = 5 см,
b = 4 см,
c = 7 см.
Найти R.
Запишем теорему синусов:
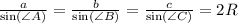
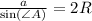
числитель и знаменатель дроби слева последнего равенства домножим на (b·c).
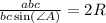
С учётом того, что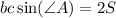 
, где S - площадь данного в условии треугольника, имеем
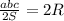
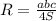
Площадь треугольника можно найти по формуле Герона:
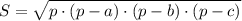, где
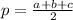
Найдем, сначала, площадь треугольника.
p = (5+4+7)/2 = (9+7)/2 = 16/2 = 8 см.
S = √(8·(8-5)·(8-4)·(8-7)) = √(8·3·4·1) = 4·(√6) см²
Теперь найдем радиус описанной окружности.
R = 5·4·7/(4·4·(√6)) = 5·7/(4·(√6)) = 35·(√6)/(4·6) = 35·(√6)/24 см.
Теперь найдём длину окружности, описанной около данного треугольника.
L = 2πR = 2π·35·(√6)/24 см = π·35·(√6)/12 см.
Проведем диагонали: AC и BD, они пересекаются в точке O, под углом 90 градусов. Наш ромб разделился на 4 равных треугольника (по свойству диагоналей в ромбе). Рассмотрим один из них, например: ABO. Угол AOB равен 90 градусам, а угол ABO возьмем за 40 градусов. Сумма углов треугольнике равна 180 градусам, проводим следующее действие: 180-(90+40)=50 градусов, мы нашли угол OAB. Вернемся к ромбу, т.к. угол OAB равен 50 градусам, угол BAD, в ромбе, равен 100 градусам. Диагональ BD делит ромб на 2 равных треугольника: BAD и BCD (значит, углы BAD и BCD равны). Сумма углов в 4-угольнике равна 360 градусам, проведем следующее действие: 360-100*2=160 градусов (осталось на углы ABC и ADC) . Углы OBA и DOE равны, как соответственные (оба по 40 градусов), проведем следующее действие: (160-40*2)/2=40 (углы BOC и AOD, опять же, как соответственные).