
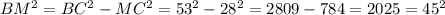 . ВМ=45.
. ВМ=45. , то отношение длин задает отношение центральных углов, которыми данные дуги определены, то есть один центральный угол будет равен 9х, а другой 11х. В сумме они дают 360 градусов, значит: 9х+11х=360, тогда 20х=360, х=18. Центральный угол, опирающийся на меньшую из дуг равен 9х=9*18=162 градуса.
, то отношение длин задает отношение центральных углов, которыми данные дуги определены, то есть один центральный угол будет равен 9х, а другой 11х. В сумме они дают 360 градусов, значит: 9х+11х=360, тогда 20х=360, х=18. Центральный угол, опирающийся на меньшую из дуг равен 9х=9*18=162 градуса.
В основании пирамиды лежит правильный треугольник ABC со стороной равной 6см.
S(осн.)= =9√3 см².
=9√3 см².
Высота правильной пирамиды падает в центр основания. Поэтому если DH высота пирамиды, а DM - апофема, то MH - радиус вписанной окружности в правильный треугольник. Т.к. по теореме о 3ёх перпендикулярах HM⊥AC.
В прямоугольном ΔDHM (∠H=90°) найдём гипотенузу DM по теореме Пифагора.
Боковые грани правильной пирамиды это равные треугольники.
S(бок.)= =9√147 см²
=9√147 см²
S(полн.) = S(осн.)+S(бок.) = 9√3 + 9√147 см²
ответ: 9√3 + 9√147 см².