ВЕ перпендикулярно AD (см чертеж) ED = BC = 10;
в прямоугольном треугольнике АВЕ ВЕ = 5;
Поэтому АЕ = 12 (теорема Пифагора), AD =АЕ + ЕD = 22;
меньшая диагональ находится из треугольника BCD с катетами 5 и 10, и равна 5*корень(5);
N - середина BC, M - срердина AD, MD = 11, NC = 5, то есть нужный отрезок находится как гипотенуза треугольника, составленного из высоты из точки N (на рисунке основание на AD буквой не обозначено, пусть это Т) и катета МТ длиной
МТ = MD - NC = 6;
MN^2 = 6^2 + 5^2 = 61. MN = корень(61);
Можно было показать, что MN = ВК, где ВК - медиана в треугольнике АВЕ. Результат получился бы таким же.
ответ не слишком красив :(((
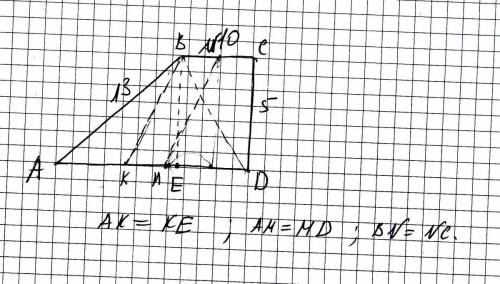
Призма АВСА1В1С1 (АВС у меня верхняя плоскость)
рассм тр АС1С:
АС1=15(по ус)
СС1=9(по ус)
по теореме Пифагора находим АС
АС=Корень(15^2-9^2)=12
Sбок=12*3*9=324 см^2
рассм тр АВС
он равносторонний,
стороны=12
чтобы найти его площадь проведем высоту ВН
рассм тр ВНС
он прямоугольный,
ВС=12
НС=12/2=6(в правильном треугольнике высота является медианой, значит АН=НС)
по теореме Пифагора найдём ВН
ВН=корень(ВС-НС)=корень(144-36)=корень(108)=6*корень(3)
SАВС=1/2АС*ВН=36*корень(3)
S пол=2*36*корень(3)+324=72*корень(3)+324