Задача на подобие треугольников и теоремы о параллельных плоскостях и прямых.
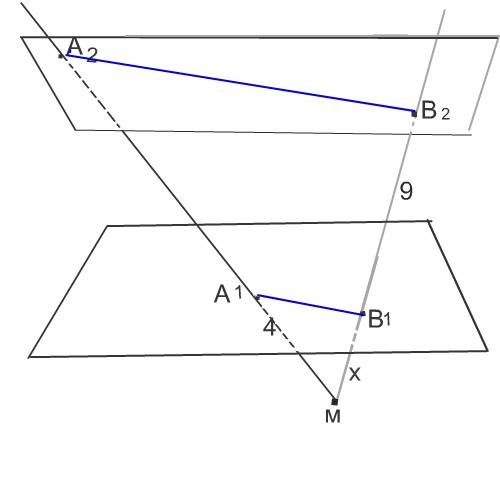
Проведем через точку М, А2 и В2 плоскость.
А1В1 параллельна А2В2 как линии пересечения параллельных плоскостей третьей плоскостью.
Остюда треугольники МА2В2 и МА1В1 подобны.
Примем отрезок МВ1 за х
Тогда МВ2=9+х,
МА2=9+х+4
4:(13+х)=х:(9+х)
36+4х=13х+х²
х²+9х-36=0
При необходимости полное решение квадратного уравнения запишете самостоятельно, а корни его 3 и -12. Второй корень не подходит.
х=3 см
МВ2=9+3=12 см
МА2=12+4=16 см
По 1 аксиоме Гильберта плоскость АВС существует,
По 3 – М и К и , соответсвенно Х принадлежат этой плоскости .
Аксиоматика Гильберта
1. Каковы бы ни были три точки A, B и C, не принадлежащие одной прямой, существует плоскость α, которой принадлежат эти три точки. Каждой плоскости принадлежит хотя бы одна точка.
2. Каковы бы ни были три точки A, B и C, не принадлежащие одной прямой, существует не более одной плоскости, которой принадлежат эти точки.
3. Если две принадлежащие прямой a различные точки A и B принадлежат некоторой плоскости α, то каждая принадлежащая прямой a точка принадлежит указанной плоскости.
4. Если существует одна точка A, принадлежащая двум плоскостям α и β, то существует по крайней мере ещё одна точка B, принадлежащая обеим этим плоскостям.
5. Существуют по крайней мере четыре точки, не принадлежащие одной плоскости.