сначала найдем cosA= корень из (1-144/169)=5/13 - отношение половины основания АВ к гипотенузе АС
АС=5/13*АВ=50*5/13=250/13
по теореме пифагора найдем СН:
СН^2=2500-62500/169=>
CH=корень из (422500-62500)/169=корень из (360000/169)=600/13
ответ: 600/13
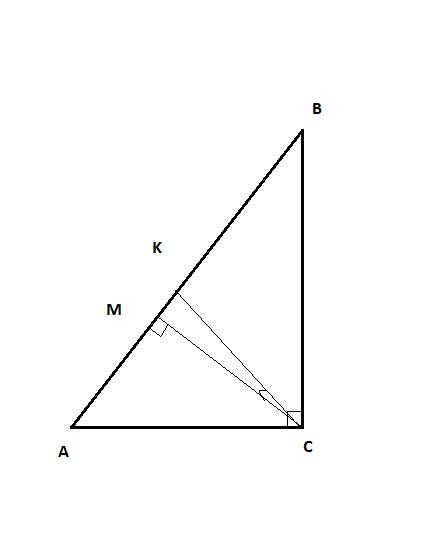
так как AC=BC то треугольник равнобедренный и CH высота и медиана ⇒ AH=HB
Синус это отношение противолежащего катета к гипотенузе.
SinA=CH/AC
12/13=CH/AC
введем x, тогда CH=12x, AC=13x
по т. Пифагора:
AH²=AC²-CH²
25²=(13x)²-(12x)²
625=169x²-144x²
625=25x²
x²=25
x=√25=5
тогда AC=13*5=64 см, CH=12*5=60 см
Выразим косинус через синус
CosA=1-(12/13)²=169/169-144/169=25/169=5/13
Косинус это отношение прилежащего катета к гипотенузе
CosA=AH/AC
5/13=25/AC
5AC=25*13
5AC=325
AC=65
по т. Пифагора:
CH²=AC²-AH²
CH²=65²-25²=4225-625=3600
CH=√3600=60 см
высота CH равна 60 см