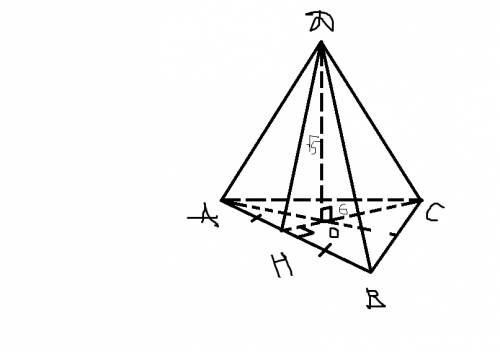
Рассмотрим треугольниу ABC-равносторонний(т.к.DABCD-прав. пирамида) OH=CH/3=6/3=2 (см)(в точке пересечения медианы делятся в отношении 2:1 от вершины)
Рассм. треуг. ODH-прямоуг. По теореме Пифагора DH=корень из DO^2+OH^2=корень из 5+4=корень из 9=3 (см)
Sпп=Sбп+Sосн
Рассм. треуг BCH-прямоуг.
sinB=MC/BC
sin60=6/BC
BC=6/(корень из 3/2)(под корнем только 3)=12/корень из 3=12 корней из 3/3=4 корня из 3(см)
Pосн=3*4 корня из 3=12 корней из 3 (см)
Sбп=1/2*DH*Pосн
Sбп=1/2*3*12 корней из 3=18корней из 3(см^2)
Sосн=1/2*CH*AB=1/2*6*4 корня из 3=12корней из3 (см^2)
Sпп=18корней из 3+12 корней из 3= 30 корней из3 (см^2)
<CAD=<BCA (как внутренние накрест лежащие при параллельных АВ и CD и секущей АС. Значит и <ВАС=30° (АС - биссектриса) и треугольник АВС равнобедренный. Тогда его высота ВН - это и медиана. Значит ВН - это часть радиуса ВО, так как радиус, перпендикулярный хорде, делит ее пополам. Угол АВС этого треугольника равен 120°. Это вписанный угол, опирающийся на дугу АDC. Значит градусная мера дуги АDC в два раза больше и равна 240°. Тогда градусная мера дуги АВС равна АВС=360°-240°=120°.
На эту дугу опирается центральный угол АОС, соответственно равный 120°. Итак, мы имеем четырехугольник АВСО, являющийся ромбом, и
точка О лежит на стороне АD нашей трапеции. Следоательно
АВ=ВС=АО=ОD=ОС=СD=R=4см. Проведем высоту трапеции СК.
В равностороннем треугольнике ОСD высота СК равна (√3/2)*а, где а=4см. СК=2√3см.
Площадь трапеции S=(BC+AD)*CК/2=12√3см².
ответ: S=12√3см².