У параллелограмма всего 4 угла. В параллелограмме есть пара острых равных между собой углов, а также пара равных тупых углов (случай прямоугольника опустим, у него все углы равны, в этой задаче такого нет). Поэтому если мы найдем острый угол, а также тупой угол параллелограмма, то мы нашли все углы.
Теперь найдем их Ситуация следующая: есть две параллельные прямые, каждая из смежных с ними сторон является секущей. Получается, что имеются две пары односторонних друг для друга углов. Рассмотрим любую из них (для второй все то же самое)
Пусть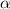 
- острый угол, 
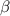- тупой. Тогда имеет место соотношение
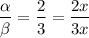
Известно, что сумма односторонних углов равна 180°, получаем вот такое уравнение:
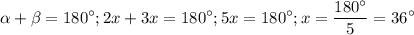
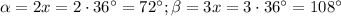
ответ: 72°, 72°, 108°, 108°
Площадь параллелограмма ABCD равна S=AD*BE, где BE- высота опущенная на сторону AD. Угол вершины A равен tg A =15/8=BE/EA, следовательно BE=15.
Таким образом S=AD*BE=10*15=150
ответ: S=150 см^2