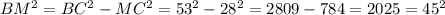 . ВМ=45.
. ВМ=45. , то отношение длин задает отношение центральных углов, которыми данные дуги определены, то есть один центральный угол будет равен 9х, а другой 11х. В сумме они дают 360 градусов, значит: 9х+11х=360, тогда 20х=360, х=18. Центральный угол, опирающийся на меньшую из дуг равен 9х=9*18=162 градуса.
, то отношение длин задает отношение центральных углов, которыми данные дуги определены, то есть один центральный угол будет равен 9х, а другой 11х. В сумме они дают 360 градусов, значит: 9х+11х=360, тогда 20х=360, х=18. Центральный угол, опирающийся на меньшую из дуг равен 9х=9*18=162 градуса.
Октаэдр представляет собой две правильные четырехугольные пирамиды с равными ребрами, приставленные друг к другу основаниями. Назовем место склейки "общим квадратом". Вершины этих пирамид проектируются в центр "общего квадрата", то есть ЛЕЖАТ на одной прямой, содержащей центр "общего квадрата". Две ДРУГИЕ диагонали октаэдра лежат в плоскости "общего квадрата" и тоже пересекаются в центре.
Поэтому в октаэдре можно провести плоскость через любые две диагонали. Одна из них - это "общий квадрат", два других таких сечения представляют собой РОМБЫ, у которых противоположные стороны параллельны.