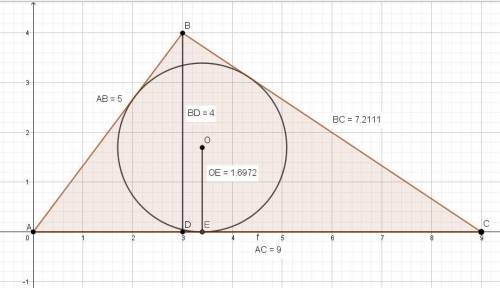
Пусть дан треугольник АВС, высота BD = 4. r = 18/(7 + √13).
Примем AD = x, CD = 2x.
Тогда сторона основания АС = 3х.
Боковые стороны: АВ = √(16 + х²), ВС = √(16 + 4х²).
Периметр треугольника Р = 3х + √(16 + х²) + √(16 + 4х²).
Площадь треугольника S = (1/2)*4*3x = 6x.
Отсюда выразим периметр через площадь и радиус вписанной окружности:
P = 2S/r = 12x/(18/(7 + √13)) = 12x(7 + √13)/18 = 2x(7 + √13)/3.
Приравняем:
3х + √(16 + х²) + √(16 + 4х²) = 2x(7 + √13)/3.
Решение уравнения: х = 3.
ответ: основание АС = 3*3 = 9.
ответ: ∠АОС=120°; Р=18
Объяснение: Центром окружности, вписанной в треугольник, является точка пересечения его биссектрис.
Сумма углов треугольника 180° ⇒ ∠САВ+∠ВСА=180°-60°=120°. Биссектрисы АО и СО делят эти углы пополам, следовательно, 0,5∠ОАС+0,5∠ОСА=120°:2=60°.
Из суммы углов треугольника угол АОС=180°-60°=120°
Стороны треугольника - касательные для вписанной окружности. Отрезки касательных от точки вне окружности до точек касания равны (свойство). ⇒ АМ=AK=4, BN=BM=2, CN=CK=3. ⇒ Р=2•(2+3+4)=18 (ед. длины)
Примечание. Обозначения в решении даны согласно условию и рисунку к нему. Но, хотя ответ тот же, по данным в условии величинам не получится построить соразмерный рисунок. Должен быть при ∠В=60° отрезок СК=2, а ВМ=3. . (См. рисунок приложения).