S1 ≈ 19,8 cм².
S2 ≈ 3,9 cм².
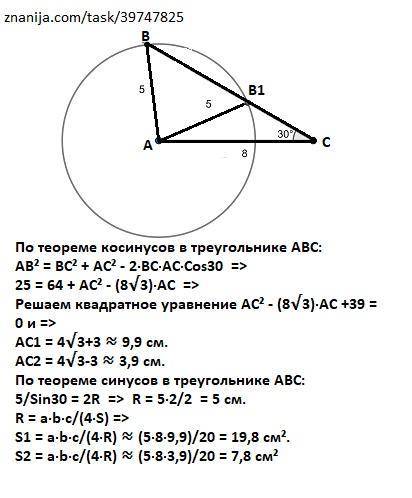
Объяснение:
По теореме косинусов в треугольнике АВС:
АВ² = ВС² + АС² - 2·ВС·АС·Сos30 =>
25 = 64 + AC² - (8√3)·AC =>
Решаем квадратное уравнение AC² - (8√3)·AC +39 = 0 и =>
AC1 = 4√3+3 ≈ 9,9 см.
АС2 = 4√3-3 ≈ 3,9 см.
По теореме синусов в треугольнике АВС:
5/Sin30 = 2R => R = 5·2/2 = 5 см.
R = a·b·c/(4·S) =>
S1 = a·b·c/(4·R) ≈ (5·8·9,9)/20 = 19,8 cм².
S2 = a·b·c/(4·R) ≈ (5·8·3,9)/20 = 7,8 cм²
P.S. Для проверки на рисунке выполнено точное построение, доказывающее, что задача имеет два решения.
№1
Дано: окружность (О; r)
∆ABC
<AOB=80°
Дуга AC : дуга BC= 2:3
Найти: все углы ∆АВС
1. Т.к <АОВ-центральный угол => градусная мера дуги, на которую он опирается,а именно дуги АВ=80°
2. Градусная мера всей окружности равна 360°. Дуга АС+Дуга ВС= 360°-80°= 280°
3. Пусть x-1 часть,тогда АС= 2х,а ВС=3х. Тогда составим и решим уравнение:
2х+3х=280°
5х=280
х= 56° => дуга АС= 56•2=112°
дуга ВС= 56•3= 168°
4. <ВСА -вписанный => градусная мера данного угла будет равна 1/2 дуги на которую он опирается => <ВСА= 1/2АВ
<ВСА= 1/2 80
<ВСА= 40°
5. <СВА-вписанный => градусная мера данного угла будет равна 1/2 дуги на которую он опирается => <СВА=1/2АС
<СВА= 1/2 112°
<СВА= 56°
6. <САВ-вписанный => градусная мера данного угла будет равна 1/2 дуги на которую он опирается => <САВ= 1/2ВС
<САВ= 1/2 168
<САВ= 84°
ответ: <СВА= 56°;
<САВ= 84°;
<ВСА= 40°
Получим 4 угла
180 - 63 = 117
то есть:
63, 63, 117, 117