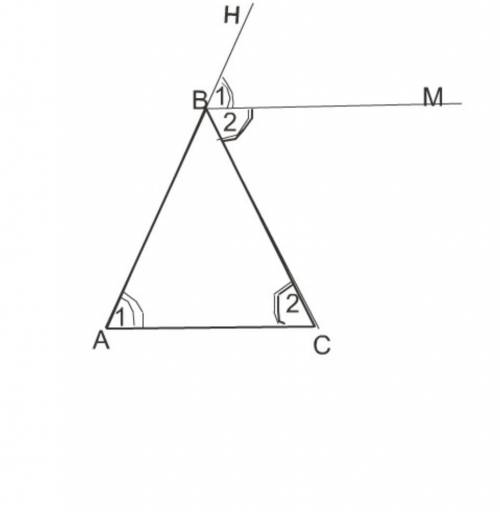
Внешний угол при вершине треугольника равен сумме внутренних углов треугольника, не смежных с ним. Рассмотрим треугольник АВС. Угол СВН - внешний угол при вершине, противоположной основанию. BM- биссектриса этого угла. Она делит угол на два равных угла 1 и 2. Так как внешний угол при В равен сумме внутренних углов А и С, а треугольник АВС равнобедренный и углы при его основании равны между собой, все выделенные углы также равны между собой. Углы под номером 1-равные соответственные при прямых АС и Bм и секущей АВ Углы под номером 2 -равные накрестлежащие при прямых АС и ВМ и секущей ВС Если при пересечении двух прямых третьей внутренние накрестлежащие углы равны, то прямые параллельны.
Самый большой угол в прямоугольном треугольнике-угол 90 градусов
Биссектриса разделила его на два равных угла
90:2=45 градусов
После проведения биссектрисы образовались два треугольника
У одного мы знаем два угла,можем узнать третий
Был треугольник АВС,проведена биссектриса СМ
В треугольнике АМС
угол АМС=74 градуса по условию задачи
угол АСМ=45 градусов
Тогда
<САМ=180-(74+45)=180-119=61 градус
Теперь рассмотрим треугольник АВС,в нем нам известны
<А=61 градус
<С=90 градусов
Сумма всех углов треугольника 180 градусов
<В=180-(61+90)=180-151=29 градусов
Треугольник СМВ
Известны 2 угла
<МСВ=45 градусов
<В=29 градусов
<СМВ=180-(45+29)=180-74=106 градусов
Объяснение:
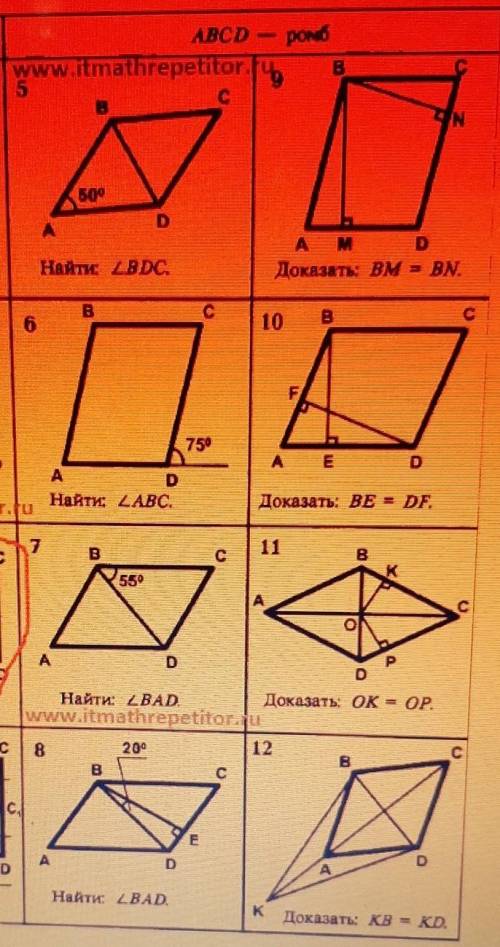
6) 105
7) 70
10) В объяснении
Объяснение:
6)
<ADC = 180 - 75 = 105
Т.к. ABCD - ромб, следует противоположные углы равны.
<ADC = <ABC = 105
7)
Т.к. ABCD - ромб, следует BC = CD
Получается BCD - равнобедренный треугольник, из чего следует, что углы <CBD = <BDC = 55
Т.к. сумма углов треугольника равна 180, следует
<BCD = 180 - <CBD - <BDC = 180 - 55 - 55 = 70
Т.к. ABCD - ромб, следует противоположные углы равны.
<BCD = <BAD = 70
10)
Углы <BAE = <FAD - т.к. это один и тот же угол.
Стороны AB = AD - т.к. это ромб.
Следует BE = DF