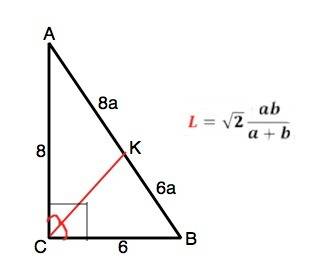
Обозначим биссектрису СК. Одно из свойств биссектрисы: отношение отрезков, на которые биссектриса делит сторону, противоположную углу, из которого проведена, равно отношению сторон, содержащих этот угол.
АК:ВК=АС:ВС
Пусть коэффициент этого отношения а.
Тогда АК=8а, ВК=6а
Отношение ВС:АС =3:4 - отношение катетов египетского треугольника, поэтому гипотенуза АВ=10 см
АВ по т.Пифагора АВ также найдем равной 10 см.
а=АВ:(8+6)=5/7 Отсюда
АК=8•4/7=40/7
sin A=BC:AB=6:10=0,6
По т.синусов
СК/sin∠CAK=AK/sin∠ACK
CK:0,6=40/7):√2/2
CK=48:7√2=24√2):7= ≈4,849 см
-------------
Примечание: для биссектрисы треугольника есть формула. В частности, для прямоугольного треугольника нахождение биссектрисы через катеты она дана в приложении с рисунком.
ABC -- нижнее основание, A1B1C1 -- верхнее основание, D -- проекция точки C1 на плоскость основания ABC, C1D -- высота призмы, C1CD=45°
AA1C1C и BB1C1C -- ромбы с острым углом 30°, AA1B1B -- квадрат
Из треугольника C1DC:
sin C1CD = C1D/C1C
sin(45°)=4*корень(2) / C1C
С1С=4*корень(2)/sin(45°)=4*корень(2)/(корень(2)/2)=4*2=8
Так как все боковые грани -- ромбы (квадрат -- это тоже ромб), то длины всех рёбер призмы равны между собой, следовательно, они равны 8.
Площадь боковой поверхности равна сумме площадей ромбов и квадрата.
Sромба=AC*AA1*sin(30°)=8*8*1/2=32
Sквадрата=AB*AA1=8*8=64
Sбок=2*Sромба+Sквадрата=2*32+64=128