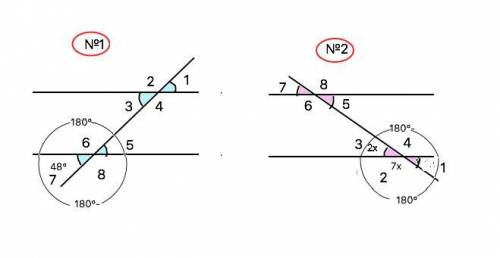
ответ: 1) меньшие по 48°, большие по 132°.
2) меньшие по 40°, большие по 140°
Объяснение: При пересечении двух параллельных прямых секущей образуется пары равных углов:
соответственные (2 и 6, 1 и 5, 3 и 7, 4 и 8).
накрестлежащие: (3 и 5, 4 и 6 - внутренние ), (2 и 8, 1 и 7 - внешние). кроме того, равны и пары вертикальных углов.
1) Как известно, сумма смежных углов равна 180°. Поэтому углы, смежные углу, равному 48°, равны 180°-48°=132°
На рисунке 1 все мéньшие углы, окрашенные голубым, равны 48°. все бóльшие - 132°
2) На рисунке 2 смежные углы 2 и 3 относятся как 2:7. Т.е. развернутый угол делится на 2+7=9 частей. Каждая часть равна 180°:9=20°. Поэтому все мéньшие углы равны 2•20°=40°, бóльшие 7•20°=140°.
ответ: 298. 32 см, 72см, 56см.
292. 23 дм.
Объяснение:
"298. Периметр треугольника равен 80 см. Стороны треугольника, образованного средними линиями данного треугольника, относятся как 4:9:7. Найдите стороны данного треугольника."
***
Пусть одна сторона треугольника, образованного средними линиями трапеции равна 4х. Тогда вторая будет 9х, а третья - 7х. Периметр этого треугольника равен 80 см.
Р=4х+9х+7х=80;
20х=80;
х=4;
4x=4*4=16 см;
9х=9*4=36 см;
7х=7*4=28 см;
Проверим:
Р=16+36+28= 80 см. Всё верно!
Средние линии треугольника равны половине основания. Значит основания равны удвоенным средним линиям.
Одна сторона равна 2*16=32 см;
Вторая сторона равна 2*36=72 см;
Третья сторона равна 2*28=56 см.
***
"292.Стороны треугольника равны 12 дм, 16 дм и 18 дм. Найдите периметр треугольника, сторонами которого являются средние линии этого треугольника."
***
АВС - треугольник. MNP - треугольник, образованный средними линиями треугольника. Каждая из них равна половине стороны ей параллельной.
MN=BC/2=16/2=8 дм.
NP=AC/2=18/2=9 дм.
MP=AB/2 =12/2=6 дм.
Р MNP=8+9+6= 23 дм.