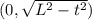Периметр равнобедренной трапеции 38 см а средняя линия 12 см найти боковую сторону

Question

Геометрия: Периметр равнобедренной трапеции 38 см а средняя линия 12 см найти боковую сторону

bigofficerjor · Accepted Answer

Поместим начало координат в вершину прямого угла, а оси направим по его сторонам. Пусть конец отрезка, который движется по оси ОХ, имеет координаты (t,0). Тогда, если длина отрезка равна L, то второй конец, который движется по оси ОY, будет иметь координаты . Тогда абсцисса середины отрезка x=t/2, а ордината середины 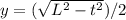. Отсюда t=2x. Подставляем это в y и получаем, что x и y  связаны соотношением 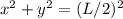. Т.е. середина отрезка описывает дугу окружности с центром в вершине прямого угла, и радиусом в половину...

MOGZ ответил