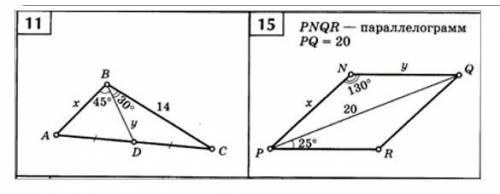
Первый признак равенства треугольников : по двум равным сторонам и равному углу между ними. В условии равные углы не образованы равными сторонами. Утверждать, что треугольники равны, нельзя (рис.1).
2. ∠BAC — прямой: ∠BAC = ∠EDF = 90°; (рис.2)
AB=DE (равные катеты); BC=EF (равные гипотенузы) ⇒
ΔABC = ΔDEF по равным катету и гипотенузе.
3. ∠BAC — тупой : ∠BAC = ∠EDF > 90°; (рис.3)
Так как в треугольнике может быть только один тупой угол, а два других будут острыми, то по теореме синусов
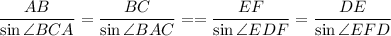
AB=DE ⇒ sin∠BCA = sin∠EFD ⇒ ∠BCA = ∠EFD (оба острые)
⇒ ∠ABC = ∠DEF (по сумме углов треугольника) ⇒
ΔABC = ΔDEF по двум равным сторонам и углу между ними.
5. ∠BCA — прямой : Так как в треугольнике может быть только один прямой угол, а два других будут острыми, то по теореме синусов
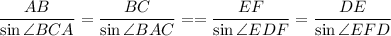
AB=DE ⇒ sin∠BCA = sin∠EFD ⇒ ∠BCA = ∠EFD = 90°
ΔABC = ΔDEF по равным катету и гипотенузе.
=====================================
Остальные дополнительные условия недостаточны - видно на рисунках.
1. ∠BAC — острый - рис.1
4. ∠BCA — острый - рис.1
6. ∠BCA — тупой - рис.4
7. AB>BC — рис.1, рис.4
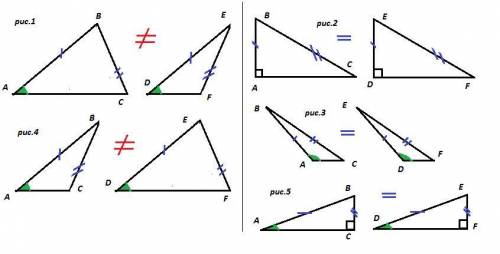
Значит, острый угол равен 180-135=45°;
Высота, боковая сторона и половина стороны, на которую опущена высота образуют прямоугольный треугольник. В этом треугольнике два острых угла равны по 45°,значит этот треугольник равнобедренный. Боковые стороны равны, значит половина стороны на которую опущена высота равна этой высоте и равна 4 см. А вся эта сторона равна 4*2=8 см;
Боковая сторона параллерограмма равна: а²=4²+4²; а=√32=4√2 см;
Периметр равен Р=8+8+4√2+4√2=16+8√2 см;
Площадь равна: S=4*8=32 см²;