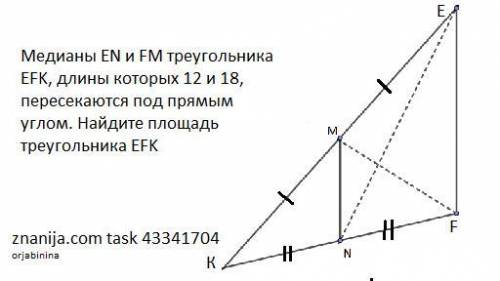
Медианы ЕN и FM треугольника EFK, длины которых 12 и 18, пересекаются под прямым углом. Найдите площадь Треугольника EFK.
Объяснение:
1) Рассмотрим выпуклый четырёхугольник EFNM у которого диагонали , по условию, взаимно- перпендикулярны .
Его площадь можно найти по формуле S = 1/2*d₁*d₂* sin (∠d₁d₂).
S(EFNM) = 1/2*12*18* sin 90°=108 ( ед²).
2) S(EFK)=S(EFNM)+S(MNK)
3) MN-средняя линия , тк M,N-середины сторон по определению медианы . По т. о средней линии треугольника MN║EF .
ΔEFK ∼ΔMNK по 2-м углам : ∠К -общий ,∠FEK=∠NMK как соответственные при MN║EF ,секущей ЕК ⇒ сходственные стороны
пропорциональны 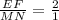 , k=
, k=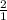 . По т об отношении площадей
. По т об отношении площадей
подобных треугольников 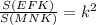 или
или 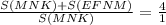 ,
,
4*S( MNK)=S(MNK)+S(EFNM) ,
3(MNK)=108 , S(MNK)=36 ед².
4) S(EFK)=S(EFNM)+S(MNK) =108+36=144 ( ед²).
1. Верные утверждения про параллелограмм:
a. Противоположные стороны параллелограмма равны
c. Противоположные углы параллелограмма равны
d. Сумма углов параллелограмма равна 360∘
e. Биссектриса угла параллелограмма отсекает от него равнобедренный треугольник
h. Точка пересечения диагоналей параллелограмма находится на равных расстояниях от противоположных вершин параллелограмма
2. Верные утверждения про прямоугольник:
a. Углы прямоугольника равны
b. Диагонали прямоугольника равны
c. Биссектриса угла прямоугольника отсекает от него равнобедренный треугольник
f. Точка пересечения диагоналей прямоугольника находится на равных расстояниях от его противоположных сторон
g. Точка пересечения диагоналей прямоугольника находится на равных расстояниях от его вершин
h. Квадрат является прямоугольником
3. Верные утверждения про ромб:
c. Биссектриса угла ромба является его диагональю
d. Точка пересечения диагоналей ромба находится на равных расстояниях от всех четырёх его сторон
e. Точка пересечения диагоналей ромба находится на равных расстояниях от его противоположных сторон
g. У всех ромбов одинаковый угол между диагоналями
h. Диагонали разбивают ромб на четыре равных треугольника
i. Квадрат является ромбом
j. Ромб, у которого равны диагонали, является квадратом
4. Верные утверждения про равнобокую трапецию:
a. В равнобокой трапеции есть равные углы
b. Диагонали равнобокой трапеции равны
e. Точка пересечения диагоналей равнобокой трапеции находится на равных расстояниях от её боковых сторон
g. Диагонали разбивают равнобокую трапецию на четыре треугольника, два из которых равны
h. Диагонали разбивают равнобокую трапецию на четыре треугольника, два из которых равнобедренные