Для решения задачи нужно знать радиус основания и высоту конуса.
Радиус найти из синуса угла а
sin а =r:L
Отсюда
r= sin а *L
Высоту конуса найдем из косинуса а
соs а=h:L
отсюда
h=соs а*L
Площадь боковой поверхности круглого конуса равна произведению половины окружности основания (C) на образующую (l)по формуле
S=1/2 C L= π r L
Sбок= π sin а *L²
Объем круглого конуса равен трети произведения площади основания S на высоту h:
V=1/3 π r² h=1/3 π( sinа *L)²▪ соs а*L=
=1/3 π▪ (sin а)² ▪ L²▪ соs а L=1/3 π ▪ sinа▪ 1/2 sin 2а ▪ L³
пришлось исправлять. Надеюсь, не напутала.
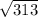
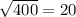
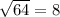
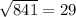
0,8
Объяснение:
1) Косинус - это отношение прилежащего катете к гипотенузе.
2) Прилежащим катетом в данном случае является высота, проведённой к основанию и боковой стороной (в данном случаем гипотенузой).
3) Так как треугольник равнобедренный, то высота ВF, опущенная из вершины В на основание АС, делит это основание на 2 равных отрезка:
АF = FC = 12 : 2 = 6 см.
4) По теореме Пифагора находим высоту BF:
BF^2 = AB^2 - AF^2 = 10^2 - 6^2 = 100 - 36 = 64
BF = √ 64 = 8 см.
5) Находим косинус угла АВF, образованного высотой ВF и боковой стороной АВ:
cos ∠ АВF = ВF : АВ = 8 : 10 = 0,8
ответ: 0,8