α = 45°
Объяснение:
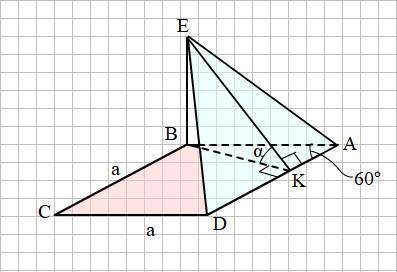
Смотри прикреплённый рисунок.
Из вершины В ромба проводим высоту ВК.
ВК = а · sin A = a · sin 60° = 0.5a√3.
Соединим точку Е с точкой К. ВК является проекцией наклонной ЕК на плоскость АВСD. Поскольку ВК - высота ромба. то ВК ⊥ AD.
По теореме о трёх перпендикулярах: если AD ⊥ BK (проекции наклонной ЕК), то AD⊥ ЕК. Следовательно, ∠ЕКВ = α является линейным углом, служащим мерой двугранного угла между плоскостями ADE и АВСD.
Найдём этот угол.
tg α = BE : BK = 0.5a√3 : 0.5a√3 = 1.
Следовательно, ∠α = 45°
Так как в треугольнике АВС АВ=ВС (боковые стороны), угол А = углу С (углы при основаниях), треугольник АВС равнобедренный. Так как биссектриса ВD проведена к основанию, то она будет являться медианой и высотой одновременно (по свойству равнобедренного треугольника). Значит, что равенство треугольников АВD и CВD можно доказать по трем сторонам, так как медиана делит основание на две равные части