1см
Объяснение:
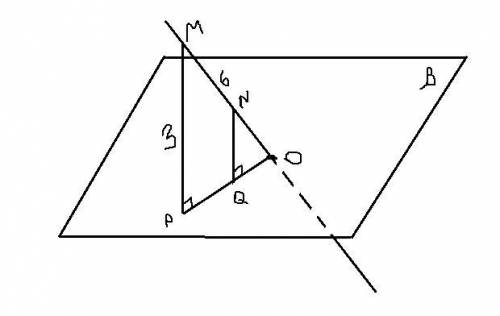
Точка N может лежать по одну сторону от плоскости β с точкой М или по другую. Если N лежит по другую сторону, то невозможно выполнить условия MN = 6 см и при этом OM = 9 см. Поэтому рассматриваем только случай, когда M и N находятся по одну сторону от плоскости β.
В этом случае расстояние от M до плоскости (определяется перпендикуляром, опущенным на эту плоскость) равно PM=3см. А расстояние от N до плоскости - QN.
Рассмотрим тр-ки MPO и NQO. Они подобны (2 угла прямые, а ещё один угол MOP общий). Значит PM/QN=OM/ON. ON=9-6=3
QN=PM*ON/OM=3*3/9=1
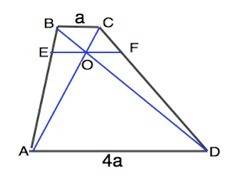
Обозначим трапецию АВСD. Пусть ВС=а, тогда АD=4а.
1) Треугольники, образованные пересекающимися диагоналями и основаниями трапеции, подобны по равным углам: вертикальные при точке пересечения О и накрестлежащие при основаниях, и k=AD:ВС=4:1⇒
АО:СО=4:1
2) Так как ЕF параллельна основаниям трапеции, ∆АВС и ∆АЕО подобны с коэффициентом подобия АО:АС,=4:(4+)=4/5
Аналогично из подобия ∆ ОDF и BDC отношение ОD:ВD=4/5
Тогда ЕО:ВС=ОF:ВС=4/5, откуда ЕО=ОF=8:2=4
Из отношения ЕО:ВС=4/5 находим ВС=5 (ед. длины)
АD=4ВС=4•5=20 (ед. длины)
———
Полезно запомнить это свойство трапеции:
Отрезок, параллельный основаниям трапеции, проходящий через точку пересечения диагоналей и соединяющий две точки на боковых сторонах, делится точкой пересечения диагоналей пополам.
1) Если т. К равноудалена от вершин правильного треугольника, то на плоскость его она проецируется в точку пересечения медиан (а также высот и биссектрис).
Медианы точкой пересечения делятся 2:1. Отрезок К1В и будет проеккией ребра КВ па пласкость треугольника.
Высота Н = Корень(12*12-6*6) = 6V3, а КВ1 = 2/3Н =4V3.
2) Ребро полученной пирамиды КВ = кор((BK1)^2 + H^2) =кор(16+48) = 8.