Відповідь:
1. 120° і 60°
2. 102° ; 78° ; 78°
3. 32° ; 32° ; 141° ; 141°
Пояснення:
1. Сума суміжніх кутів = 180°
Нехай один кут=1х ; другий кут=2х
Рівняння: х+2х=180° ; 3х=180° х=180:3=60°
Перший кут=1х=60°
Другий кут=2х=2•60°=120°
Перевірка:60°+120°=180°
2.
1 варіант:
Суміжний йому кут=180°-102°=78°
Два вертикальні кути=102°
Два інші вертикальні кути=78°
2 варіант:
Вертикальний йому кут теж=102°
Сума двох інших вертикальних кутів=360°-(102°•2)=156
Один з двох вертикальних кутів=156:2=78°
3.
Дані кути не є суміжними, а є вертикальними, оскільки сума зуміжних кутів=180°
Один з двох даних кутів=78°:2=39°
Суміжний йому кут=180°-39°=141°
Вертикальний знайденому куту теж=141°
Сподіваюся, я вам допоміг.
Вибачте, якщо не розумієте українську.
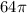 см³.
см³.
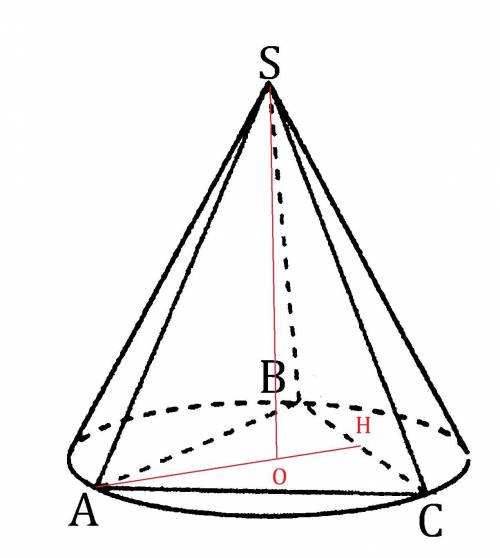
Обозначим данную пирамиду буквами 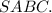
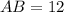 см.
см.
Проведём высоту пирамиды SO.
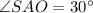
Начертим около этой пирамиды конус.
Так как конус описан около данной пирамиды, то высота конуса совпадает с высотой данной пирамиды.
=======================================================
Так как данная пирамида - правильная, треугольная ⇒ основание данной пирамиды - правильный треугольник.
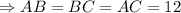 см.
см.
Проведём высоту  в
в 
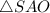 - прямоугольный, так как
- прямоугольный, так как 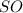 - высота пирамиды.
- высота пирамиды.
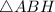 - прямоугольный, так как
- прямоугольный, так как  - высота
- высота  .
.
Так как  - равносторонний ⇒
- равносторонний ⇒  - высота, медиана и биссектриса
- высота, медиана и биссектриса
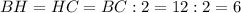 см, так как
см, так как  - медиана.
- медиана.
Найдём  по теореме Пифагора
по теореме Пифагора 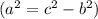 .
.
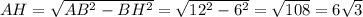 см.
см.
Точка 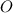 - пересечение медиан и делит их в отношении
- пересечение медиан и делит их в отношении 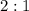 , считая от вершины.
, считая от вершины.
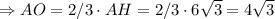 см
см
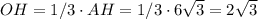 см.
см.
Также 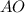 - радиус описанной около
- радиус описанной около  окружности.
окружности.
Рассмотрим 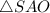
Если угол в прямоугольном треугольнике равен 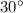 , то напротив лежащий катет равен половине гипотенузы.
, то напротив лежащий катет равен половине гипотенузы.
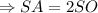
Составим уравнение:
Пусть 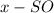 , тогда
, тогда  .
.
И по теореме Пифагора 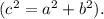
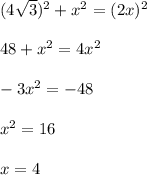
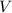 конуса =
конуса = 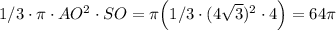 см³.
см³.
Samt = 1 1/3 ед².
Объяснение:
По теореме Менелая для треугольника АВС и секущей ЕМ:
(СЕ/ЕВ)·(ВК/КА)·(АМ/(МС) =1. => (4/1)·(5/2)·(АМ/(АМ+9√2)) = 1. =>
10АM/(AM+9√2) = 1. => АМ = √2. CA/АM = 9/1. => АС/СМ = 9/10.
По теореме Менелая для треугольника МВА и секущей ТС:
(МТ/ТВ)·(ВК/КА)·(АС/(СМ) =1. =>
(МТ/ТВ)·(5/2)·(9/10)) = 1. => МТ/ТВ = 4/9. => МТ/МВ = 4/13.
Треугольники МВА и АМТ - треугольники с одной высотой, то есть отношение их площадей равно отношению сторон, на которую проведена высота. =>
Samt/Smba = 4/13.
Smba = (1/2)·АВ·MA·Sin(ВАМ). ∠ВАМ = 45° (как смежный с ∠ВAС = 135°).
Smba = (1/2)·7·√2·√2/2 = 3,5 ед². =>
Samt = (4/13)·3,5 = 1 1/13 ед².