Question

1. Найти площадь треугольника, если его стороны 4 и 7 см, а угол между ними 30 градусов. 2. Найти площадь ромба, сторона которого равна 5 корней из 3 см, а один из углов 150 градусов.

Answer 1

Задача 1 - ответ: 7 см².

Задача 2 - ответ: 37,5 см².

Объяснение:

Задача 1.

Площадь треугольника равна половине произведения сторон треугольника на синус угла между ними:

S = (4*7*sin30°) :2 = (28*0,5) : 2 = 7 см².

ответ: 7 см².

Задача 2.

Сумма углов ромба, прилегающих к одной его стороне, равна 180°. Поэтому если один угол равен 150°, то второй угол равен 30°.

Так как ромб состоит из двух равновеликих треугольников, то его площадь можно выразить как удвоенное произведение площади одного треугольника, равную половине произведения двух сторон ромба на синус угла между ними:

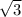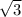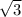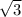S = [(5$\sqrt{3}$ * 5$\sqrt{3}$ *sin30°) :2] * 2 = 5$\sqrt{3}$ * 5$\sqrt{3}$ *sin30° = 25*3*0,5 = 37,5 см².

ответ: 37,5 см².