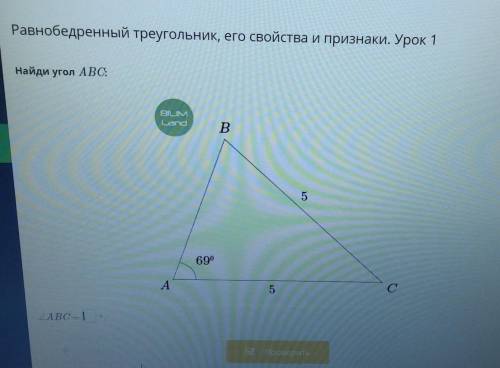
АС=ВС, трикутник АВС-рівнбедренний
кут АВС= кутВАС(за ознакою: в рівнобедреному трикутнику кути при основі рівні)
Отже кутАВС=69°
Ромб - это параллелограмм, у которого все стороны равны (докажите сами). То есть ромб является параллелограммом.
<AOE = <ACB (как соответственные углы при ||-ных прямых OE и BC и их секущей AC).
Тогда треугольники ACB и AOE подобны по двум углам (<A=<A, <AOE=<ACB),
тогда их стороны пропорциональны, то есть:
AC/AO = BC/EO = AB/AE. (*)
Треугольники AOB и COD равны (докажите сами), тогда
AO = CO, тогда
AC/AO = (AO+CO)/AO = 2AO/AO = 2.
Тогда из (*):
2 = BC/EO, отсюда EO = (1/2)*BC,
Но у ромба все стороны равны, то есть BC = DC, поэтому
EO = (1/2)*BC = (1/2)*DC.
Ч. т. д.
1)Раз АВ = 7, то и СD = 7, диагонали в точке пересечения делятся пополам. В итоге: АО = 3, ВО = 5, АВ = 7. ответ: 3+5+7=15 см
2)Площадь трапеции вычисляется по формуле: (ВС+АД)/2×ВН. на рисунке изображена равнобедренная трапеция: АВ=СД=4. Проведём из вершин В и С две высоты к нижнему основанию АД: ВН и СК. Они делят АД так что ВС=НК=5, а АН=КД. Рассмотрим полученный ∆АВН. Он прямоугольный и в нём АН и ВН- катеты, а АВ - гипотенуза. <А=60°, а сумма острых углов прямоугольного треугольника составляет 90°, поэтому <АВН=90–60=30°. Катет АН, лежащий напротив угла 30° равен половине гипотенузы, поэтому АН=АВ÷2=4÷2=2.
Теперь найдём ВН по теореме Пифагора:
ВН ²=АВ²–АН²=4²–2²=16–4=12; ВН=СК=√12=2√3
Если АН=КД=2, а НК=5, тогда
АД=2×2+5=4+5=9.
Теперь найдём площадь трапеции зная её высоту и оба основания:
S=(5+9)/2×2√3=14÷2×2√3=14√3
Объяснение:
я не умею но решение по теме
по идее тоже 69
Объяснение:
Так как это равнобедренный треугольник, а сторона АВ и АС боковые