Объяснение:
Проведём перпендикуляр в точке О. Я его назвал H1H2. Точка О лежит на средней линии трапеции (так как концы этого отрезка на серединах сторон). Средняя линия параллельна основаниям (такое свойство у средней линии трапеции). Значит H1H2 перпендикулярно и средней линии и основаниям.
Докажем, что H1O=H2O, это можно сделать по теореме Фалеса, утверждающей, что параллельные прямые отсекают на секущих равные отрезки, (отрезки на боковой стороне равны, значит и на перпендикуляре равны).
И теперь рассматриваем треугольники AOH2 и COH2, о чудо они равны по 2 углам и стороне между ними (OH2=OH1, только что доказали, угол AH2O=OH1C=90 (там перпендикуляры), угол AOH2=COH1 как вертикальные)
А если треугольники равны, то и стороны против равных углов в них равны (есть такая теорема) значит и AO=OC равны ч.т.д.
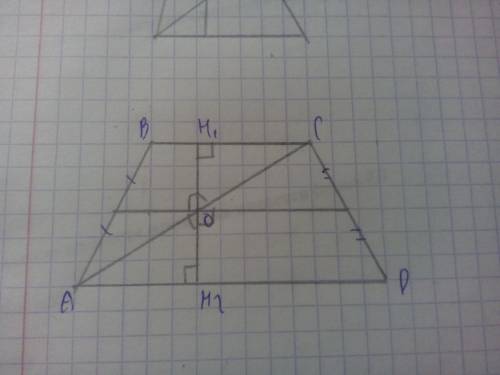
См. чертеж.
К - середина АС. Поскольку центр SAC лежит на SK на расстоянии SK/3 от К, то искомое расстояние равно 2/3 от KQ, где KQ перпендикуляр к SP (необходимые перпендикулярности всех прямых и плоскостей докажите сами, там все просто), Р - середина MN.
Если ребро пирамиды a = 6, то PN = a/4; (тут была ошибка! - приношу извинения)
SN = a√3/2;
Отсюда SP = √(SN^2 - PN^2) = a√(3/4 - 1/16) = a√11/4;
Прямоугольные треугольники SOP и PQK имеют общий острый угол KPS, поэтому они подобны.
Поэтому SO/SP = KQ/КР;
SO - это высота тетраэдра, SO = a√(2/3);
КР = a√3/4 (половина высоты грани)
получается
KQ = (a√(2/3)) (a√3/4)/(a√11/4) = a√(2/11);
Соответственно, искомое расстояние от центра грани SAC до KP (то есть до плоскости SMN, что то же самое - это надо доказать тоже) равно (2/3)KP = 2a√(2/11)/3 = 4√(2/11);
Численно √(2/11) = 0,4264.... с точностью до 5 знака после запятой (именно так :)) Но это все-таки лучше, чем первоначальный ответ, в котором катет KQ был больше гипотенузы KP.