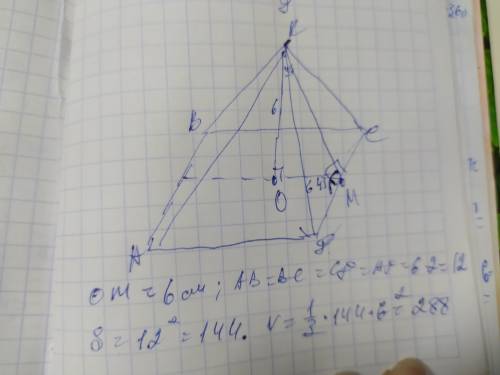
Обозначим вершины пирамиды АВСД, высоту КО, а апофему КМ. Соединим точки О и М и получим прямоугольный треугольник КМО, в котором высота КО и ОМ - катеты, а КМ - гипотенуза. Сумма острых углов прямоугольного треугольника составляет 90° и если угол КМО=45°, то угол МКО=90-45=45°. Этот треугольник равнобедренный, поэтому КО=МО=6см. В основании правильной четырёхугольной пирамиды лежит квадрат. Если МО=½ ВС, поэтому АВ=ВС=СД=АД=6×2=12см
Sосн=а², где а- сторона основания. Найдём по этой формуле площадь основания: S=12²=144см²
Теперь найдём объем пирамиды по формуле: V=⅓×Sосн×KO=⅓×144×6=288см³
ОТВЕТ: V=288см³
ответ: 72π см2
Объяснение:
Дано:
Sо.с. - 0,6 см2
h - 0,1 см2
Sп.п.-?
Площадь основания вычисляется по формуле:
Sосн. = πr2
Площадь боковой поверхности конуса равна произведению половины окружности основания а на образующую
Sбок.=1/2*а* l=π r l
Полная площадь поверхности конуса
Sп.п.=Sбок. + Sосн.=π r l+π r2 = πr (r + l)
Вычислим сначала радиус r
Площадь сечения конуса - это площадь двух прямоугольных треугольников с равными катетами
Sо.с.= rh/2 + rh/2=2rh/2=rh
r = Sо.с./h=0,6/0,1=6 см
Находим образующую l
l2=r2+h2=6^2 +0, 1^2 = 36+0,01= 36,01 см2
l=√36,01=6 см
Площадь полной поверхности конуса:
Sп.п. = π 6 (6+6) =72 π cм2