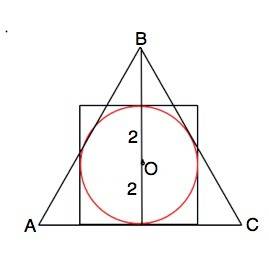
1. Правильный четырехугольник - квадрат.
Диаметр вписанной в квадрат окружности равен стороне квадрата. ⇒ r=d:2=4:2=2 см.
Для описанного вокруг данной окружности треугольника АВС она - вписанная.
Радиус вписанной в правильный треугольник окружности равен 1/3 его высоты. Следовательно, высота ∆ АВС =2•3=6 см.
Тогда АВ=ВН:sin60°=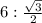
=4√3 см.
* * *
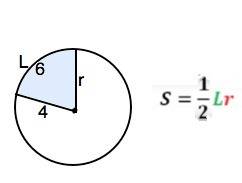
2. Для нахождения площади сектора существует формула.
S=Lr:2, где L – длина дуги сектора. ⇒
S=6•4:2=12 см²
Если формула забыта, решить задачу можно без нее.
Длина окружности C=2πr
C=2•p•4=8π см
Площадь окружности S=πr²=16 π см²
Вычислим площадь, которая приходится на сектор с дугой в 1 см.
S:C=16π:8π=2
Тогда площадь сектора
S=2•6=12 см²
1. R - радиус описанной окружности
a-сторона правильного треугольника
стороны правильного треугольника равны 45/3=15см
a/sin(pi/3)=2*R
так же радиус можно найти по формуле R=b/(2*sin(pi/N))
b- сторона правильного многоугольника
N- количсетво углов в многоугольнике (равно количеству сторон)
приравниваем две формулы, выражаем b.
2. площадь квадрата равна квадрату его стороны, значит сторона квадрата равны корню квадратному из 72
опять используем известную уже формулу радиуса описанной окружности, R=b/(2*sin(pi/N)) и найдём радиус окружности.
площадь круга равна pi*R^{2} (число пи умноженнное на квадрат радиуса)
4. необходимо использовать формулы из задачи 1.
5. площадь вписанного 6_угольника S=(3sqrt{3}*a^{2})/2, отсюда находим сторону а и используем ее в следуещей формуле, откуда мы находим радиус окружности R=а/(2*sin(pi/N))
l=2*pi*R - длина окружности
6. площадь сектора находится по формуле S=frac{pi*R^{2}*alpha}{360}
Чтобы найти расстояние между параллельными прямыми, выберите на одной из них произвольную точку и опустите перпендикуляр на другую (вторую) прямую. Затем измерьте длину полученного отрезка. Длина перпендикуляра, соединяющего две параллельные линии и будет расстоянием между этими линиями.
2Так как на практике на чертеже всегда представлены не самипрямые, а лишь их отрезки, то точку на первой прямой (отрезке этой прямой) выбирайте так, чтобы второй конец перпендикуляра попал на отрезок второй прямой.
3Для того чтобы провести перпендикуляр, возьмите чертежный инструмент «треугольник» с прямым углом. Выбрав точку на первой прямой, приложите к ней одну из примыкающих к прямому углу сторон треугольника (катет), а второй катет совместите со второй прямой. Теперь, просто проведите линию вдоль первого катета, пока она не достигнет второй прямой.
4Чтобы измерить длину полученного перпендикуляра, возьмите циркуль. Совместите ножки циркуля с точками пересечения перпендикуляра с прямыми. Теперь переместите ножки циркуля на измерительную линейку.
5Если циркуля нет, то просто совместите нулевое деление измерительной линейки с началом перпендикуляра и расположите линейку вдоль него. То деление, рядом с которым будет располагаться вторая точка пересечения и будет длиной перпендикуляра, а следовательно и расстоянием между параллельными прямыми.