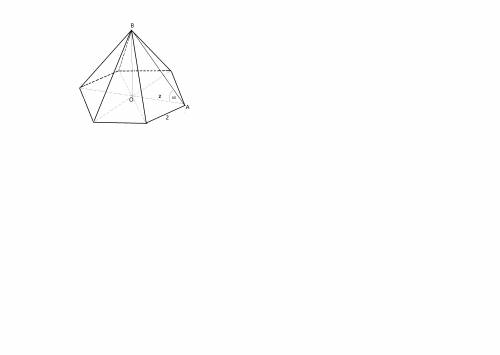
Смотри вложение, Lanovaya. Там в чертеже чуть неправильно, а остальное верно. Неверно в биссектрисах.
Объем пирамиды равен одной трети произведения ее высоты на площадь основания.
V=⅓ S∙h
Основание правильного шестиугольника состоит из шести правильных треугольников.
Площадь правильного треугольника находят по формуле:
S=(а²√3):4
S=4√3):4=√3
Площадь правильного шестиугольника в основании пирамиды:
S=6√3
Высоту найдем из прямоугольного треугольника АВО:
Так как ребро образует с с диагональю основания угол 60°, высота пирамиды ВО равна
H=ВО=2:ctg (60°)= 2·1/√3=2√3
Можно найти высоту и по т. Пифагора с тем же результатом.
V= 2√3∙6 √3:3=12 (кубических единиц)
Трапеция АВСД, проводим биссектрису угла В до пересечения с АД точка Н -пересечение, угол АНВ=углу НВС как внутренние разносторонние=углу АВН, трекгольник АВН равнобедренный AF - биссектриса=высоте=медиане
треугольник АFВ прямоугольный АВ-гипотенуза= корень (АF в квадрате +ВF в квадрате)=
=корень (576+100)= 26