2) дуга АВ = 104°
3) CD = 4,2 см
периметр ∆CОD = 12,6 см
Объяснение:
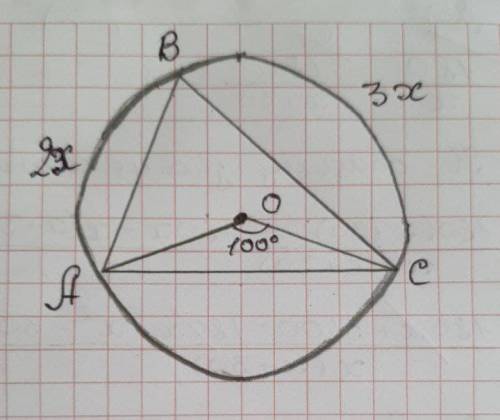
2) ∠АОС - центральный угол окружности с центром О.
Градусной мерой дуги окружности называется градусная мера соответствующего ей центрального угла , т.е. Длина дуги АС=100°
∪АВ:∪ВС=2:3 ⇒ ∪АВ=2х, ∪ВС=3х
т.к. в окружности 360°, составляем уравнение:
∪АС+∪АВ+∪ВС=360°
100+2х+3х=360
5х=260
х=52°
∪АВ=2х = 2*52=104°
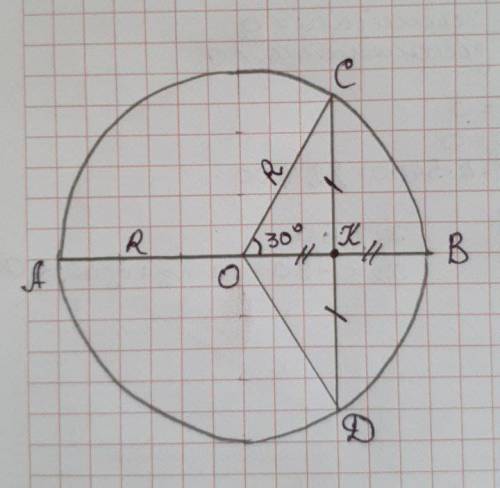
3) Радиус = половине диаметра: R= 1/2 * АВ = 8,4*1/2=4,2
К - середина хорды CD ⇒ СК=КД
Угол между диаметром и радиусом это угол СОК.
Рассмотрим ΔСОК и ΔДОК : ОС=ОД - радиусы окружности, ОК - общая, СК=ДК - по условию ⇒ ΔСОК = ΔДОК по трём сторонам (3 признак равенства треугольников)
Из равенства Δ следует равенство углов: ∠СОК=∠ДОК = 30° ⇒∠СОД=60°
∠С = ∠Д = (180°-60°)/2= 60°
т.к. ∠С = ∠Д = ∠О ⇒ ΔСОД - равносторонний ОС=ОД=СД=R = 4,2
РΔ=3*R =3*4,2=12,6 см
Рассмотрим образованную пирамиду АВСК. КВ перпендикулярно АВС, значит нам необходимо найти длину высоты, опущенной в грани АСК из вершины К на АС. По теореме о трех перпендикулярах ее проекция на плоскость АВС будет перпендикулярна АС. Обозначим точку пересечения высоты с АС через Н. Тогда нужно найти КН.
Рассмотрим основание пирамиды - треугольник АВС. Он равнобедренный АС=ВС=10, с углом у основания А=30 градусов. Опустим высоту из вершины треугольника С на АВ - СМ. Высота, опущенная из точки С, будет и биссектрисой, и медианой треугольника. То есть АМ=МВ. Треугольник АСМ - прямоугольный, с одним из осмтрых углов = 30 градусов, значит катет, лежащий против этого угла, равен половине гипотенузы: АМ=1/2*АС, АМ=1/2*10=5 (см). По теореме Пифагора найдем второй катет СМ:
CM=sqrt(AC2-AM2)
CM=sqrt(100-25)=sqrt75=5sqrt3
BH- проекция КН на плоскость основания АВС, и, как было уже отмечено, ВН перпендикулярна АС. Рассм отрим треугольники АНВ и АМС- они подобны:
АН/АМ=НВ/МС=АВ/АС
НВ/МС=АВ/АС
НВ=МС*АВ/АС
НВ=5*(2*5sqrt3)/10=5sqrt3
Треугольник КНВ - прямоугольный (КВ перпендикулярно плоскости АВС). По теореме Пифагора найдем КН:
KH2=KB2+HB2
KH=sqrt(25+75)=sqrt100=10 (см)