Во-первых, чтобы найти периметр параллелограмма нужно умножить сумму двух непараллельных сторон на 2.
Во-вторых, если Р - середина стороны BC, то BP = PC = 6. И значит, BC = BP+PC = 12.
В третьих, получившийся треугольник OPC - прямоугольный( так как египетская тройка), поэтому OC = 5 см.
В четвёртых, диагонали точки пересечения делятся по полам. Значит AO = OC = 5 см.
Потом, треугольник ABO подобен OCD ( ABO = COD ( вертик); и пара накрест лежащих углов). Значит, коэффициент подобия равен 5. А AB = CD = 5.
Все, можно найти периметр: (12 + 5) • 2 = 34 см.
ответ: периметр 38 см.
9,6π см³
Объяснение:
Объяснение: Фигура, которая получается вращением прямоугольного треугольника около гипотенузы, имеет веретенообразную форму, т.е. вид двух конусов с общим основанием. Объём этой фигуры равен сумме объёмов этих двух конусов
. Формула объема конуса V=H•S/3, где Н - высота конуса, Ѕ - площадь основания.
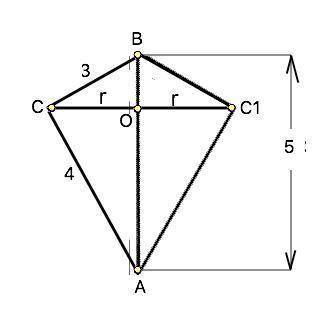
Рассмотрим рисунок с осевым сечением фигуры вращения.
Образующая конуса (CBC₁) – катет ВС=3, высота ВО=h₁, r=CО; образующая конуса (САС₁) - катет АС=4, высота АО=h₂, r=OC.
V(кон₁)=πr²•h₁/3
V(кон₂)=πr₂•h₁/3
V(кон₁)+V(кон₂)=πr²•(h₁+h₂)/3
h1+h2=AB - гипотенуза ∆ АВС,
По т.Пифагора АВ=√(AC²+BC²)=√(3²+4²)=5 см
r=CO=BC•AC:AB=3•4:5=2,4 см
V₁+V₂=π•2,4²•5/3=9,6π см³
==============================
Объяснение: