ответ: АК = СК = 5 см
Объяснение:
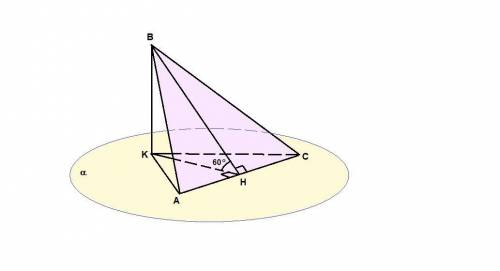
ВК⊥α, тогда АК и СК - проекции боковых сторон треугольника АВС на плоскость α.
Пусть Н - середина АС. Тогда ВН - медиана равнобедренного треугольника, проведенная к основанию, значит является и высотой,
ВН⊥АС,
КН - проекция ВН на плоскость α, значит КН⊥АС по теореме о трех перпендикулярах, тогда
∠ВНK = 60° - линейный угол двугранного угла между плоскостью АВС и плоскостью α.
ΔАВН: ∠АНВ = 90°, АВ = √73 см, АН = АС/2 = 3 см,
по теореме Пифагора
ВН = √(АВ² - АН²) = √(73 - 9) = √64 = 8 см
ΔВКН: ∠ВКН = 90°,
cos∠BHK = KH / BH
KH = BH · cos∠BHК = 8 · 1/2 = 4 см
ΔАКН: ∠АНК = 90°, по теореме Пифагора
АК = √(КН² + АН²) = √(16 + 9) = √25 = 5 см
Если равны наклонные, проведенные из одной точки, то равны и их проекции:
СК = АК = 5 см
Значит, РС+AD=2·15
РС+25=30
РС=5
ВС=ВР+РС
25=ВР+5
ВР=25-5=20
∠PAD=∠BPA - внутренние накрест лежащие при параллельных ВС и AD и секущей АР.
∠ВАР=∠РАD - биссектриса АР делит угол А пополам.
Значит ∠BPA =∠ВАР и треугольник АВР - равнобедренный АВ=ВР=20
Противоположные стороны параллелограмма равны CD=AB=20
Из треугольника АСD по теореме косинусов:
АС²=AD²+DC²-2·AD·DC·cos ∠D
(5√46)²=25²+20²-2·25·20·cos ∠D
1150=625+400-1000·cos ∠D
cos ∠D =-0,125
Противоположные углы параллелограмма равны
∠В=∠D
Из треугольника АBP по теореме косинусов:
АP²=AB²+BP²-2·AB·BP·cos ∠B
АP²=20²+20²-2·20·20·(-0,125)
АP²=400+400+100
АP²=900
AP=30
Р( трапеции АРСD)= АР+РС+СD+AD=30+5+20+25=80
ответ. Р=80