В правильном многоугольнике все стороны и углы равны.
Внутренний угол правильного n-угольника вычисляется по формуле
ΔABC = ΔBCD по двум сторонам и углу между ними (AB=BC=CD, ∠ABC=∠BCD), поэтому AC=BD, как соответственные стороны (AC напротив ∠ABC; BD напротив ∠BCD и эти углы равны).
ΔABD = ΔDCA по трём сторонам (AB=DC, AC=DB и AD - общая), поэтому ∠BAD=∠CDA, как соответственные углы (∠BAD напротив BD; ∠CDA напротив AC и эти стороны равны).
Сумма углов в выпуклом четырёхугольнике равна 360°.
Обозначим неизвестные стороны параллелепипеда: АА1 = х, АД = у. Если диагонали BD1 и A1C взаимно перпендикулярны, то они определяют фигуру - ромб. Диагональ боковой грани А1В - это гипотенуза в треугольнике А1ОВ и равна √(3²+4²) = 5 см. В свою очередь А1В =√(3²+х²). Приравняем √(3²+х²) = 5 3²+х² = 25 х² = 25-9 = 16 х = 4 см. В ромбе А1ВСД1 сторона А1В равна ребру параллелепипеда А1Д1 и равна 5 см. Диагональ основания ВД = √(ВД1²-х²) = √(36-16) = √20 = 2√5 = 4.472136 Площадь основания равна двум площадям треугольника АВД, которую определяем по формуле Герона: So =2√(р(р-a)(p-b)(p-c)) =2*6.6332 = 13.2665 см², здесь р = 6.236068 см, a = 3 cм, в = 5 см, с = 4.472136 см. Тогда объём параллелепипеда V = So*x = 13,2665*4 = 53.066 cм³.
В правильном многоугольнике все стороны и углы равны.
Внутренний угол правильного n-угольника вычисляется по формуле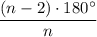
ΔABC = ΔBCD по двум сторонам и углу между ними (AB=BC=CD, ∠ABC=∠BCD), поэтому AC=BD, как соответственные стороны (AC напротив ∠ABC; BD напротив ∠BCD и эти углы равны).
ΔABD = ΔDCA по трём сторонам (AB=DC, AC=DB и AD - общая), поэтому ∠BAD=∠CDA, как соответственные углы (∠BAD напротив BD; ∠CDA напротив AC и эти стороны равны).
Сумма углов в выпуклом четырёхугольнике равна 360°.
В четырёхугольнике ABCD:
∠ABC+∠BCD+∠CDB+∠DAB = 360°
2·(∠BCD+∠CDA) = 360°
∠CDA = 360°:2-∠BCD = 180°-144° = 36°
ответ: 36°.