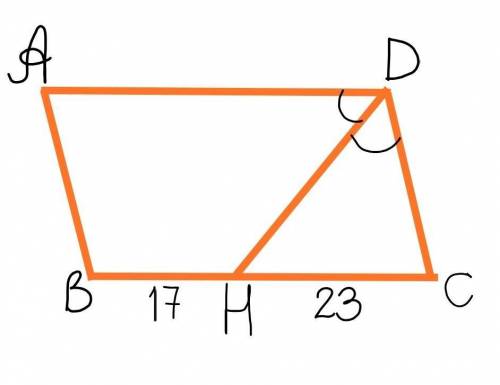
Так как противоположные стороны параллелограмма параллельны, то угол СНD=угол ADH как накрест-лежащие при параллельных прямых AD u BC и секущей DH.
Биссектриса делит угол на два равных угла.
Следовательно угол СDH=угол ADH.
Исходя из найденного: Угол СHD=угол CDH.
Тогда ∆CHD – равнобедренный с основанием HD.
У равнобедренного треугольника боковые стороны равны, тоесть CD=CH=23 см
Противоположные стороны параллелограмма попарно равны.
Следовательно: AD=BC=BH+HC=17+23=40 см; AB=CD=23 см.
Периметр параллелограмма – это сумма длин всех его сторон.
Тоесть Р=AD+AB+BC+CD=40+23+40+23=126 см.
ответ: 126 см.
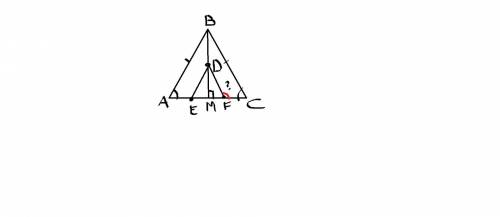
Угол CFD = 130°
Объяснение:
Треугольник ABC - равнобедренный ⇒ углы при основании будут равны, также как и стороны.
BM является биссектрисой, медианой и высотой, а значит угол BMF будет равен 90°
Нам известно, что угол FDE равен 80°
Так как BM - биссектриса, то она делит этот угол пополам, а значит угол FDM равен 40°
Рассмотрим треугольник FDM:
Угол DMF = 90° ;
Угол FDM = 40° ;
Угол DMF будет равен: 180° - 90° - 40° = 50°
А теперь мы можем дать ответ:
Угол CFD будет равен: 180° - ∠DFM, то есть 180° - 50° = 130°.
Площади подобных фигур относятся как квадрат коэффициента подобия. S1:S2=k²=64/25
Пусть одна часть этого отношения равна х. Тогда
64х-25х=39х
39х=156
х=4 см
S1=4•64=256 см²
S2=4•25=100 см²
S1-S2=256-100=156 cм²