Дано :
трапеция ABCD ( AD BC )
∠A = ∠B =90° ; °
CH ⊥ AD ;
∠D =45° ;
а) AH =4 м ; DH =1 м ;
или
б) AH =1 м ; DH =4 м.
——————————
AB -? ; BC -? ; CD -? ; AD -?
Решение(Доказательство):
а)
Из прямоугольного треугольника CHD :
CH = DH = 1 м т.к. ∠D =∠DCH =45° ⇒ CD= √(CH²+DH)²=√2 (м) .
AB = CH = 1 м ; BC =AH = 4 м ;AD=AH м. + DH м. =4 м. +1 м. =5 м .
S =((AD +BC)/2 ) * CH =((5+4)/2)* 1 = 4,5 (м² ) .
б)
CH = DH = 4 м т.к. ∠D =∠DCH =45°⇒ CD= CH√2 =4√2 ( м) .
AB = CH = 4 м ; BC =AH = 1 м ;AD=AH + DH =1 м. +4 м. =5 м .
S =((AD +BC)/2 ) * CH =((5+1)/2)* 4 = 12 (м² ) .
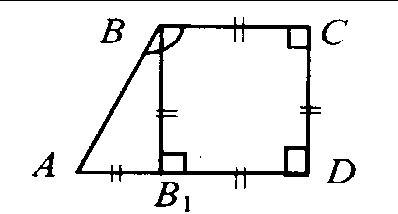
Рассмотрим четырёхугольник ABCD.
По условию задачи имеем:
AB = BC и AD = DC.
Опустим высоту BH треугольника ABC из вершины B на основание AC.
Так как AB = BC, то треугольник ABC - равнобедренный и высота BH является одновременно и медианой, т.е. AH = CH.
Аналогично опустим высоту DG треугольника ADC из вершины D на основание AC.
Так как AD = DC, то треугольник ADC - равнобедренный и высота DG является одновременно медианой, т.е. AG = CG.
Так как AH = CH и AG = CG, то точки H и G совпадают.
BH и DG перпендикулярны AC и точки H и G совпадают.
Следовательно, BH и DG лежат на прямой перпендикулярной AC и BD является диагональю четырехугольника ABCD.
Итак получили, что диагонали AC и ВD перпендикулярны, что и требовалось доказать.
можете не благодарить
Да, могут.
Объяснение: