1) Треугольники вне восьмиугольника равны по двум сторонам и углу между ними(по свойству правильного многоугольника), значит стороны вписанного многоугольника равны, а т.к. его стороны равны, то это правильный восьмиугольник.
2)В треугольнике АВМ:АД-высота(т.к.угол АДМ=90), также АД является медианой этого треугольника(ВД=МД по условию) из этого следует, что треугольник АВМ-равнобедренный. Тогда АВ=АМ=4. И т.к. АМ=МС, АС=АМ+МС=4+4=8.
3)Треугольники вне восьмиугольника равны по двум сторонам и углу между ними(по свойству правильного многоугольника), значит стороны вписанного четырехугольника равны, и это значит, что это четырехугольник-ромб, т.к. диагонали правильного восьмиугольника равны, то и в ромбе диагонали равны, из чего следует, что это квадрат.
4)Обозначим СД=х.Проведем высоты ВН1 и СН2, угол ДСН2=90-60=30. Тогда ДН2=1/2 СД=х/2. Т.к. АД=2х, то АН1=2х-х-х/2=х/2, из этого следует, что трапеция равнобедренная, а значит СД=2. Тогда АД=2СД=2*2=4. СН2=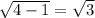
. S=СН2*АД=корень из 3*4=4 корня из 3
ответ: например
Объяснение:Cos (a+b)=cos(a-(-b))=cos a*cos(-b)+sin a*sin (-b)= cos a*cos b-sin a*sin b значит cos(a+b)=cos a*cos b- sin a*sin b. Докажем формулу (4): sin. (a+b)=cos(пи/2-(a+b))=cos((пи/2-a)-b)=cos(пи/2-a)cos b+sin(пи/2-a)sin b=sin a*cos b+cos a*sin b Значит sin (a+b)=sin a*cos b+sin b*cos a Докажем формулу (3) Применяя последнюю формулу имеем sin(. ... ф-ция y=cos x-четная. Из формул сложения пологая b=пи n/2, где n ÎN, можно вывести формулы привидения для преобразований выражений вида cos(пи*n/2 ±a), sin(пи*n/2 ±a). Например cos(пи*n/2 -a)= cos пи/2*cos a+sin пи/2*sin a=0+sin a=sin a. Аналогично выводятся следующие формулы: Sin.