Нет
Объяснение:
Сумма углов выпуклого многоугольника находится по формуле S = (n-2)*180°, где n - количество углов или сторон многоугольника.
Найдем по формуле сумму углов выпуклого семиугольника: S = (7 - 2)*180° = 5*180° = 900°.
Допустим, что наименьший угол 136°. Допустим, что все остальные углы равны, тогда они больше 136° на величину x°.
Тогда получим: 136° + 6*(136° + x°) = 900°
136° + 816° + 6x° = 900°
6x° = 900° - 952°
6x° = -52°
x =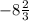 
°, т.е. получаем противоречие, т.к. x - отрицательно, т.е остальные углы в таком случае меньше 136°, а значит 136° не наименьший угол.
ответ: нет
площадь треугольника acd= (ad*dc)/2=28 cм2. Если ad взять за x то cd за x+1 т. к. противоположные стороны равны. Потом из формулы площади составляем уравнение x2+x-56=0. Подходит только корень 7 из этого следует что ad=bc=7 ab=cd=8 периметр 8*2+7*2=30см